题目内容
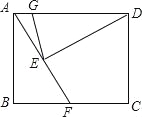
【题目】如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
(1)求证:DF⊥AB;
(2)利用图中阴影部分面积完成勾股定理的证明,已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.

【答案】见解析
【解析】试题分析:(1)、首先证明△ABC和△DEC全等,从而得出∠BAC=∠EDC,根据∠EDC+∠CED=90°,∠CED=∠AEF,从而得出∠AEF+∠BAC=90°,即垂直;(2)、根据![]() ,然后将各线段的长度代入即可得出答案.
,然后将各线段的长度代入即可得出答案.
试题解析:解:(1)∵△ABC≌△DEC,
∴∠BAC=∠EDC,
∵∠EDC+∠CED=90°,∠CED=∠AEF,
∴∠AEF+∠BAC=90°,
∴∠AFE=90°,
∴DF⊥AB.
(2)∵S△BCE+S△ACD=S△ABD﹣S△ABE,
∴![]() a2+
a2+![]() b2=
b2=![]() cDF﹣
cDF﹣![]() cEF=
cEF=![]() c(DF﹣EF)=
c(DF﹣EF)=![]() cDE=
cDE=![]() c2,
c2,
∴a2+b2=c2

练习册系列答案
相关题目