题目内容
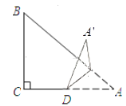
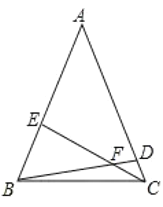
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,若
上的点,若![]() ,
,![]() ,
,![]() ,则
,则![]() ______.
______.
【答案】![]()
【解析】
分别作CH⊥AB,BG⊥AC,与AB交于H,与AC交于G,证明△BHC≌△CGB,可得BH=CG,HC=BG,证明Rt△HEC≌Rt△GDB,可得HE=DG,再根据![]() ,
,![]() 可得HE=DG=1,BH=CG=3,再在Rt△ABG中,根据勾股定理可求得BG,在Rt△BGD中,根据勾股定理可求得BD.
可得HE=DG=1,BH=CG=3,再在Rt△ABG中,根据勾股定理可求得BG,在Rt△BGD中,根据勾股定理可求得BD.
解:如下图,分别作CH⊥AB,BG⊥AC,与AB交于H,与AC交于G,
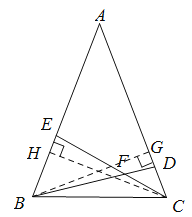
∵CH⊥AB,BG⊥AC
∴∠BHC=∠BGC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△BHC和△CGB中
∵
∴△BHC≌△CGB(AAS)
∴BH=CG,HC=BG,
在Rt△HEC和Rt△GDB中
∵![]()
∴Rt△HEC≌Rt△GDB(HL)
∴HE=DG,
∵![]() ,
,![]()
∴BH+HE=4,CG-DG=2,
∴HE=DG=1,BH=CG=3,
∵![]() ,
,
∴AG=AC-CG=7,
∴在Rt△ABG中,根据勾股定理
![]() ,
,
在Rt△BGD中,根据勾股定理
![]() .
.
故答案为:![]()

练习册系列答案
相关题目
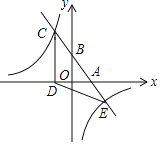
【题目】吴京同学根据学习函数的经验,对一个新函数y=![]() 的图象和性质进行了如下探究,请帮他把探究过程补充完整
的图象和性质进行了如下探究,请帮他把探究过程补充完整
(1)该函数的自变量x的取值范围是 .
(2)列表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … |
| m | ﹣1 |
| ﹣5 | n | ﹣1 |
|
| … |
表中m= ,n= .
(3)描点、连线
在下面的格点图中,建立适当的平面直角坐标系xOy中,描出上表中各对对应值为坐标的点(其中x为横坐标,y为纵坐标),并根据描出的点画出该数的图象:
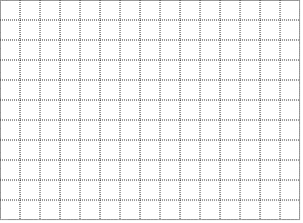
(4)观察所画出的函数图象,写出该函数的两条性质:
① ;
② .