题目内容
【题目】阅读下面材料:
如图1,已知线段AB、CD相交于点O,且AB=CD,请你利用所学知识把线段AB、CD转移到同一三角形中。
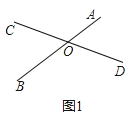
小强同学利用平移知识解决了此问题,具体做法如下:
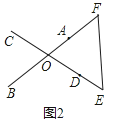
如图2,延长OD至点E,使DE=CO,延长OA至点F,使AF=OB,连接EF,则△OEF为所求的三角形。
请你仔细体会小强的做法,探究并解答下列问题:
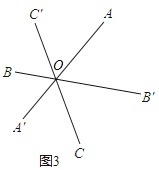
如图3,长为2的三条线段AA′,BB′,CC′交于一点O,并且∠B′OA=∠C′OB=∠A′OC=60°;
(1)请你把三条线段AA′,BB′,CC′ 转移到同一三角形中。(简要叙述画法)
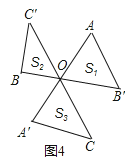
(2)连接AB′、BC′、CA′,如图4,设△AB′O、△BC′O、△CA′O的面积分别为S1、S2、S3,则S1+S2+S3________(填“>”或“<”或“=”)。
【答案】![]()
【解析】试题分析:(1)根据材料得出延长OA至点E,使AE=A′O;延长OB′至点F,使B′F=OB;连接EF,则△OEF为所求;
(2)根据平移的性质首先得出![]() ,再利用图象得出S1+S2+S3<S△EOF.
,再利用图象得出S1+S2+S3<S△EOF.
试题解析:
(1)如图所示:画法:①延长OA至点E,使AE=A′O;②延长OB′至点F,使B′F=OB;③连接EF,则△OEF为所求的三角形。
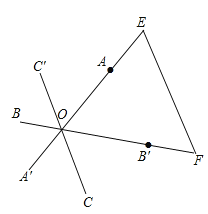
(2)∵长为2的三条线段AA′,BB′,CC′交于一点O,
并且∠B′OA=∠C′OB=∠A′OC=60°;
∴△OEF为边长为2的等边三角形,∴![]() ,
,
在EF上截取EQ=CO,则QF=C′O,
∴可得△A′CO≌△QEA,△B′FQ≌△OBC′,
如图所示:
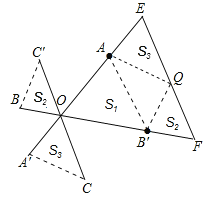
则![]() 。
。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中五次行驶纪录如下。(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
-4 | +7 | -9 | +7 | -2 |
(1)求第二次记录时距A地多远?
(2)在第______次纪录时距A地最远。
(3)若每千米耗油0.8升,问共耗油多少升?