题目内容
【题目】某校园商店经销甲、乙两种文具. 现有如下信息:

请根据以上信息,解答下列问题:
(1)甲、乙两种文具的零售单价分别为 元和 元.(直接写出答案)
(2)该校园商店平均每天卖出甲文具50件和乙文具120件.经调查发现,甲种文具零售单价每降0.1元,甲种文具每天可多销售10件.为了降价促销,使学生得到实惠,商店决定把甲种文具的零售单价下降m(m>0)元.在不考虑其他因素的条件下,当m定为多少时,可以使商店每天销售甲、乙两种文具获取的利润保持不变?
【答案】(1)、2元和3元;(2)、0.5元时获利170元.
【解析】
试题分析:(1)、根据题意得出甲、乙零售单价;(2)、根据题意列出关于m的一元二次方程,从而求出m的值得出答案.
试题解析:(1)、甲、乙零售单价分别为2元和3元;
(2)、![]() 即
即![]() ,
,
解得m= 0.5或m=0(舍去)
答:当m定为0.5元才能使商店每天销售甲、乙两种商品获取的利润共170元。

练习册系列答案
相关题目
【题目】在如图中,每个正方形有边长为1 的小正方形组成:
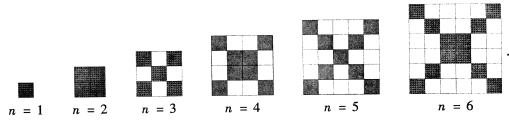
(1) 观察图形,请填写下列表格:
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 | … | |||||
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 | … |
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1,白色小正方形的个数为P2,问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.