题目内容
【题目】如图在Rt△ABC中，∠BAC=90 o，AC=2AB，点D是AC的中点,将一块锐角为45 o的直角三角板如图放置，使三角板斜边的两个端点分别与A，D重合，连接BE，EC。试猜想线段BE和EC的数量及位置关系，并证明你的猜想。
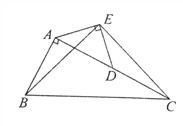
【答案】BE=EC且BE⊥EC，证明见解析.
【解析】试题分析：数量关系为：BE=EC，位置关系是：BE⊥EC；利用直角三角形斜边上的中线等于斜边的一半，以及等腰直角三角形的性质，即可证得：△EAB≌△EDC即可证明．
试题解析：BE=EC BE⊥EC
证明∵AC=2AB，点D是AC的中点
∴AB=AD=CD
∵∠EAD=∠EDA=45°
∴∠EAB=∠EDC=135°
∵EA=ED
∴△EAB≌△EDC
∴∠AEB=∠DEC，EB=EC
∴∠BEC=∠AED=90°
∴BE=EC，BE⊥EC
练习册系列答案
相关题目
