��Ŀ����
����Ŀ��С����Сǿ��ij���μ����ʵ������ó��ðװ�ֽ����װ�У�ÿ�Űװ�ֽ�ɲó�3��������5���иǣ���һ�������������и�ǡ��������һ����װ�У���óɺ����İװ�ֽ��x�ţ���ش��������⣺
(1)����11�Űװ�ֽ��
��������±���
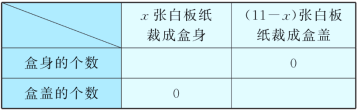
���ʣ����������ٸ���װ�У�
(2)���ֿ�������4��������3���иǺ�23�Űװ�ֽ���ְѰװ�ֽ�ֳ������֣�һ���ֲóɺ�����һ���ֲóɺиǣ���������и�ȫ����������ʱ���������ٸ���װ�У�
(3)����n�Űװ�ֽ(70��n��80)���Ȱ�һ�Űװ�ֽ�ó�2��������1���и�(����һ��߽��ϲ�Ҫ)��ʣ�°װ�ֽ�ֳ������֣�һ���ֲóɺ�����һ���ֲóɺиǣ���������и�ȫ����������ʱ��n��ֵ������______��
���𰸡���1���ټ���������������15����װ�У���2������34����װ�У���3��72.
��������
(1) ����x�Ű�ֽ������,���У�11-x�������и�,����ÿ�Űװ�ֽ�ɲó�3��������5���иǣ����ɽ��
�ڸ���һ�������������и�ǡ��������һ����װ�е÷��̣�
��2������y�Űװ�ֽ�óɺ������������е�4��������3���иǣ�����һ�������������и�ǡ��������һ����װ�е÷��̣�
��3������z�Űװ�ֽ�óɺ����������⣬�÷���2��(3z��2)��1��5(n��z��1)������z��nΪ���������.
(1)��������£�
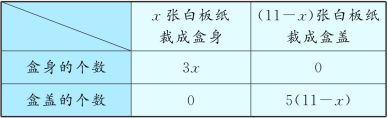
�������⣬��2��3x��5(11��x)�����x��5.
�����飬x��5��ԭ���̵Ľ⣬�ҷ������⣮
��3x��15.
��������15����װ�У�
(2)����y�Űװ�ֽ�óɺ����������⣬��
2��(3y��4)��3��5(23��y)�����y��10.
�����飬y��10��ԭ���̵Ľ⣬�ҷ������⣮
��3y��4��34.
�𣺿���34����װ�У�
(3)����z�Űװ�ֽ�óɺ����������⣬��
2��(3z��2)��1��5(n��z��1)��
���z��![]() .
.
��z��������
��5n��8Ϊ11�ı�����
�֡�70��n��80��nΪ��������
��n��72.

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�