题目内容
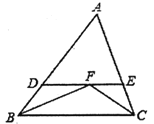
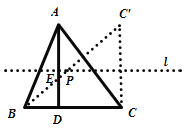
【题目】如图，△ABC中，AD垂直BC于点D，且AD=BC，BC上方有一动点P满足
，则点P到B、C两点距离之和最小时，∠PBC的度数为（ ）
A.30°B.45°C.60°D.90°
【答案】B
【解析】
根据
得出点P到BC的距离等于AD的一半，即点P在过AD的中点且平行于BC的直线l上，则此问题转化成在直线l上求作一点P，使得点P到B、C两点距离之和最小，作出点C关于直线l的对称点C’，连接BC’，然后根据条件证明△BCC’是等腰直角三角形即可得出∠PBC的度数．
解：∵，
∴点P到BC的距离=
AD，
∴点P在过AD的中点E且平行于BC的直线l上，
作C点关于直线l的对称点C’，连接BC’，交直线l于点P，
则点P即为到B、C两点距离之和最小的点，
∵AD⊥BC，E为AD的中点，l∥BC，点C和点C’关于直线l对称，
∴CC’=AD=BC，CC’⊥BC，
∴三角形BCC’是等腰直角三角形，
∴∠PBC=45°．
故选B．
练习册系列答案
相关题目
