题目内容
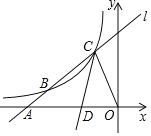
【题目】已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示．有下列结论：①b2﹣4ac＞0；②abc＞0；③8a+c＞0；④9a+3b+c＜0；⑤（a+c）2＜b2．其中，正确结论的个数是（ ）
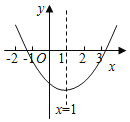
A.2B.3C.4D.5
【答案】C
【解析】
抛物线有两个交点，
＞0，①正确；抛物线开口、对称轴和y轴的交点可以判断出a＞0，b＜0，c＜0，②正确；③中没有b，可以用对称轴
，即b=-2a，替换掉b，把x=-2代入函数，可得8a+c＞0；③正确；④中a的系数为9，可以考虑到把x=3代入后得到，其对应的y值小于0，故④正确；考虑到⑤中出现两个平方，且系数都为1，把x=±1代入后相乘可得到（a+b+c）（a+b-c）=
＞0，所以⑤正确．
解：抛物线与x轴有两个不同的交点，因此b2﹣4ac＞0，故①正确；
抛物线开口向上，因此a＞0，对称轴为x＝1＞0，a、b异号，因此b＜0，抛物线与y轴交在负半轴，因此c＜0，所以abc＞0，故②正确；
由图象可知，当x＝﹣2时，y＝4a﹣2b+c＞0，又对称轴x＝﹣
＝1，即，b＝﹣2a，所以8a+c＞0，故③正确；
当x＝3时，y＝9a+3b+c＜0，因此④正确；
当x＝1时，y＝a+b+c＜0，当x＝﹣1时，y＝a﹣b+c＜0，所以（a+b+c）（a﹣b+c）＞0，即（a+c）2﹣b2＞0，也就是（a+c）2＞b2，故⑤错误，
综上所述，正确结论有：①②③④
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
【题目】光明中学全体学生900人参加社会实践活动，从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图，结合图中所给信息解答下列问题：
填写下表：
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
估计光明中学全体学生社会实践活动成绩的总分．
