题目内容
【题目】已知，如图
中，
，
是边
上一点，
，过点
三点的
交
于点
，点
在
上，连接
(1)求证：
是等腰三角形；
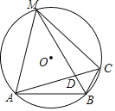
(2)若
，请用题意可以推出的结论说明命题：“一组对边相等，且一组对角相等的四边形是平行四边形”是假命题
【答案】（1）见解析；（2）见解析
【解析】
（1）由等腰三角形的性质得到
，再由圆内接四边形性质得到∠BFD=∠ACB，从而有∠BFD=∠B，即可证出结论；
（2）用已知AB=DE, ∠B=∠E，可推出四边形ABDE是平行四边形是假命题
证明
∵四边形AFDC是⊙o的内接四边形，
∴∠AFD+∠C=180°
∵∠BFD+∠AFD=180°
∴∠BFD=∠ACB
∴∠BFD=∠B
∴△BDF是等腰三角形；
（2）解：如图，已知AB=DE, ∠B=∠E，则四边形ABDE是平行四边形是假命题.
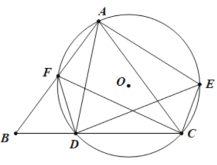
理由：
但四边形ABDE不是平行四边形.故四边形ABDE是平行四边形是假命题.
练习册系列答案
相关题目
