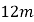Question

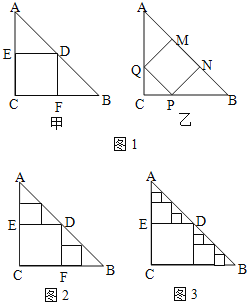
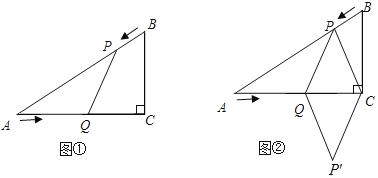
【题目】已知：如图①，在Rt△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜4），解答下列问题：

（1）当t为何值时，PQ∥BC；

（2）设△AQP的面积为y（cm2），求y与t之间的函数关系式；

（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；

（4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．

Answer 1

【答案】（1）；（2）y＝﹣t2+6t．（3）不存在t的值使线段PQ恰好把Rt△ACB的周长和面积同时平分；（4）t＝s

【解析】

（1）只要证明△APQ∽△ABC，可得=，构建方程即可解决问题；（2）过点P作PE⊥AC于E，则有△APE∽△ABC，由相似三角形的性质构建二次函数即可解决问题；（3）由题意可求Rt△ACB的周长和面积，当线段PQ恰好把Rt△ACB的周长平分，可得AP+AQ＝×24＝12，可求t的值，代入y与t之间的函数关系式，可求出y≠12，则不存在t的值使线段PQ恰好把Rt△ACB的周长和面积同时平分；（4）连接P'P交AC于点O，由△APO∽△ABC，可得=，即=，可得AO＝，由菱形的性质可得OQ＝OC，构建方程即可解决问题．

解：（1）在Rt△ABC中，AB＝ ＝＝10（cm），

∵点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；

∴BP＝t，AQ＝2t，则AP＝10﹣t，

∵PQ∥BC，

∴△APQ∽△ABC，

∴=

∴=

∴t＝

∴当t＝s时，PQ∥BC．

（2）如图，过点P作PE⊥AC于点E，

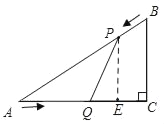
∵PE⊥AC，BC⊥AC，

∴PE∥BC，

∴△APE∽△ABC，

∴=，

∴=，

∴PE＝6﹣t，

∴y＝×2t×（6﹣t）＝﹣t2+6t．

（3）∵∠C＝90°，AC＝8cm，BC＝6cm，AC＝10cm，

∴△ABC的周长为24cm，△ABC的面积为24cm2，

∵线段PQ恰好把Rt△ACB的周长平分，

∴AP+AQ＝×24＝12，

∴10﹣t+2t＝12，

∴t＝2，

当t＝2时，y＝﹣×4+12≠×24，

∴不存在t的值使线段PQ恰好把Rt△ACB的周长和面积同时平分．

（4）如图，连接P'P交AC于点O，

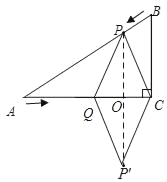
∵四边形PQP′C为菱形

∴PO⊥AC，OQ＝OC，

∴PO∥BC，

∴△APO∽△ABC，

∴=，，

∴=，，

∴AO＝ ，

∵OQ＝OC，

∴AO﹣AQ＝AC﹣AO，

∴2×﹣2t＝8，

∴t＝，

∴当t＝s时，四边形PQP′C为菱形．