题目内容
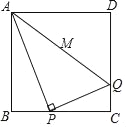
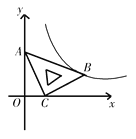
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),AB=![]() ,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
【答案】![]()
【解析】
过点B作BD⊥x轴于点D,在Rt△ABC中利用勾股定理求出AC的长,在Rt△OAC中利用勾股定理求出OA的长,然后证明△OAC≌DCB,可得BD,CD的长,即可得点B的坐标,最后利用待定系数法即可求出反比例函数的解析式.
解:过点B作BD⊥x轴于点D,

在Rt△ABC中,AC=BC,AB=![]() ,
,
由勾股定理可得AC=BC=2,
∵点C的坐标为(1,0),
∴OC=1,
在Rt△OAC中,
OA=![]() =
=![]() =
=![]() .
.
∵∠OCA+∠DCB=90°,∠OCA+∠OAC=90°,
∴∠OAC=∠DCB,
在△OAC和△DCB中,
 ,
,
∴△OAC≌△DCB,
∴CD=OA=![]() ,BD=OC=1,
,BD=OC=1,
∴OD=CD+OC=![]() +1,
+1,
即点B的坐标为(![]() +1,1).
+1,1).
设反比例函数的解析式为y=![]() ,
,
则1=![]() ,
,
解得k=![]() +1,
+1,
所以反比例函数的解析式为y=![]() .
.
故答案为:y=![]() .
.

 全能练考卷系列答案
全能练考卷系列答案【题目】某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点.从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求
总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01