题目内容
【题目】我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.

(1)已知凸五边形![]() 的各条边都相等.
的各条边都相等.
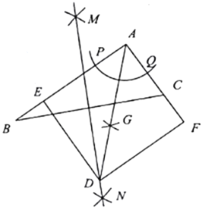
①如图1,若![]() ,求证:五边形
,求证:五边形![]() 是正五边形;
是正五边形;
②如图2,若![]() ,请判断五边形
,请判断五边形![]() 是不是正五边形,并说明理由:
是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”)
如图3,已知凸六边形![]() 的各条边都相等.
的各条边都相等.
①若![]() ,则六边形
,则六边形![]() 是正六边形;( )
是正六边形;( )
②若![]() ,则六边形
,则六边形![]() 是正六边形. ( )
是正六边形. ( )
【答案】(1)①证明见解析②若![]() ,五边形
,五边形![]() 是正五边形(2)①真命题②真命题
是正五边形(2)①真命题②真命题
【解析】
(1)①用SSS证明![]() ,得到
,得到![]() ,即可得证;
,即可得证;
②先证![]() ,再证明
,再证明![]() ,再根据四边形的内角和与平行的性质证得
,再根据四边形的内角和与平行的性质证得![]() 即可得证;
即可得证;
(2)①先证![]() ,设
,设![]() ,
,![]()
![]() ,根据x,y的等量关系求出
,根据x,y的等量关系求出![]() ,
,![]() ,从而求出
,从而求出![]() ,故可得到结论;
,故可得到结论;
②连接![]() 、
、![]() 、
、![]() ,先证
,先证![]() ,再证
,再证![]() ,得到
,得到![]() ,再由①可得出结论.
,再由①可得出结论.
(1)①证明:∵凸五边形![]() 的各条边都相等,
的各条边都相等,
∴![]() ,
,
在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
∴五边形![]() 是正五边形;
是正五边形;
②解:若![]() ,五边形
,五边形![]() 是正五边形,理由如下:
是正五边形,理由如下:
在![]() 、
、![]() 和
和![]() 中,
中,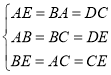 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,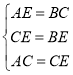 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵四边形![]() 内角和为
内角和为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理:![]() ,
,
∴五边形![]() 是正五边形;
是正五边形;
(2)解:①若![]() ,如图3所示:
,如图3所示:
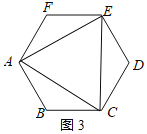
则六边形![]() 是正六边形;真命题;理由如下:
是正六边形;真命题;理由如下:
∵凸六边形![]() 的各条边都相等,
的各条边都相等,
∴![]() ,
,
在![]() 、
、![]() 和
和![]() 中,
中,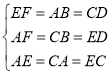 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,
,![]()
![]() ,
,
则![]() ①,
①,![]() ②,
②,
①+②得:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴六边形![]() 是正六边形;
是正六边形;
故答案为:真;
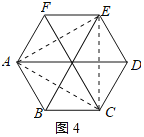
②若![]() ,则六边形
,则六边形![]() 是正六边形;真命题;理由如下:
是正六边形;真命题;理由如下:
如图4所示:连接![]() 、
、![]() 、
、![]() ,
,
在![]() 和
和![]() 中,
中,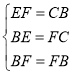 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,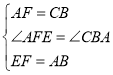 ,
,
∴![]() ,
,
∴![]() ,
,
同理:![]() ,
,
∴![]() ,
,
由①得:六边形![]() 是正六边形;
是正六边形;
故答案为:真.

练习册系列答案
相关题目