题目内容
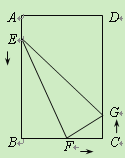
【题目】(12分)如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点
A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速
度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后
第ts时,△EFG的面积为Scm2.
(1)当t=1s时,S的值是多少?
(2)写出S与t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点B、E、F为顶点的三角形与以C、F、G为顶点的三角形相似?请说明理由。
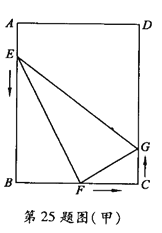
【答案】解:(1)如图(甲),当![]() 秒时,AE=2,EB=10,BF=4,FC=4,CG=2
秒时,AE=2,EB=10,BF=4,FC=4,CG=2
由![]()
=![]()
(2)①如图(甲),当![]() 时,点E、F、G分别在边AB、BC、CD上移动,
时,点E、F、G分别在边AB、BC、CD上移动,
此时![]()
![]()
![]()
即![]() (
(![]() )
)
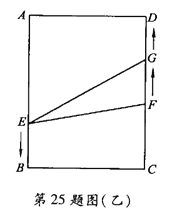
②如图(乙)当点F追上点G时,![]() ,解得
,解得![]() .
.
当![]() 时,点E在边AB上移动,点F、G都在边CD上移动.
时,点E在边AB上移动,点F、G都在边CD上移动.
此时CF=![]() .CG=
.CG=![]() .
.
FG=CG-CF=![]()
![]()
即![]() (
(![]() )
)
(3)如图(甲),当点F在矩形的边BC上移动时,![]() .
.
在△EBF和△FCG中,∠B=∠C=90°.
①若![]() .即
.即![]() ,解得
,解得![]() 。
。
又![]() 满足
满足![]() ,所以当
,所以当![]() 时,△EBF∽△FCG.
时,△EBF∽△FCG.
②若![]() .即
.即![]() ,解得
,解得![]() 。
。
又![]() 满足
满足![]() ,所以当
,所以当![]() 时,△EBF∽△GCF.
时,△EBF∽△GCF.
综上所述,当![]() 或
或![]() 时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似.
时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似.
【解析】略

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目