题目内容
【题目】如图,![]() 是圆
是圆![]() 的直径,
的直径,![]() ,点
,点![]() 是圆
是圆![]() 上一动点(与
上一动点(与![]() ,
,![]() 不重合),
不重合),![]() 的平分线交圆
的平分线交圆![]() 于
于![]() .
.
![]() 判断
判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
![]() 若
若![]() 是
是![]() 的内心,当点
的内心,当点![]() 运动时,
运动时,![]() 、
、![]() 中是否存在长度保持不变的线段?如果存在,请指出并求其长度;如果不存在,请说明理由.
中是否存在长度保持不变的线段?如果存在,请指出并求其长度;如果不存在,请说明理由.

【答案】(1)△ABD是等腰直角三角形,理由见解析;(2)![]() 的长度不变,且
的长度不变,且![]() .
.
【解析】
(1)先根据圆周角定理得出∠ADB=90°,根据CD平分∠ACB可知![]() ,所以AD=BD,故可得出结论;
,所以AD=BD,故可得出结论;
(2)先根据勾股定理求出BD的长,连接BI,则∠4=∠5,由(1)可知![]() ,所以∠1=∠2,再由三角形外角的性质可知∠3=∠1+∠4=∠2+∠5,故可得出DI=BD是定值.
,所以∠1=∠2,再由三角形外角的性质可知∠3=∠1+∠4=∠2+∠5,故可得出DI=BD是定值.
解:![]() 是等腰直角三角形.理由如下:
是等腰直角三角形.理由如下:
∵![]() 是圆
是圆![]() 的直径,
的直径,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
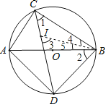
(2)![]() 的长度不变,且
的长度不变,且![]()
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
连接![]() ,
,
∵![]() 是
是![]() 的内心,
的内心,
∴![]() ,
,
∵由![]() 可知
可知![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,
,
∴![]() 是定值,即
是定值,即![]() .
.

练习册系列答案
相关题目
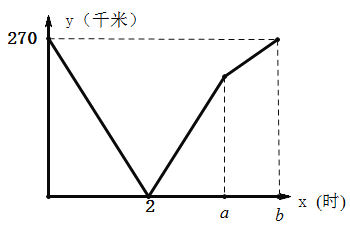
【题目】某共享单车公司提供了手机和会员卡两种支付方式.若用手机支付方式,骑行时间在半小时以内(含半小时)不收费,超出半小时后每半小时收费1元,若选择会员卡支付,骑行时间每半小时收费0.8元,设骑行时间为x小时.
(1)根据题意,填写下表(单位:元):
骑行时间(小时) | 0.5 | 2 | 3 | … |
手机支付付款金额(元) | 0 | … | ||
会员卡支付付款金额(元) | 3.2 | … |
(2)设用手机支付付款金额为y1元,用会员卡支付付款金额为y2元,分别写出y1,y2关于x的函数关系式;
(3)若李老师经常骑行该公司的共享单车,他应选择哪种支付方式比较合算?