题目内容
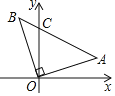
【题目】如图,等腰Rt△OAB,∠AOB=90°,斜边AB交y轴正半轴于点C,若A(3,1),则点C的坐标为_____.
【答案】(0,![]() )
)
【解析】
过B作BE⊥y轴于E,过A作AF⊥x轴于F,根据全等三角形的性质得到B(﹣1,3),设直线AB的解析式为y=kx+b,求得直线AB的解析式为y=﹣![]() x+
x+![]() ,于是得到结论.
,于是得到结论.
过B作BE⊥y轴于E,过A作AF⊥x轴于F,如图所示:
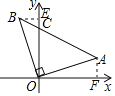
∴∠BCO=∠AFO=90°,
∵A(3,1),
∴OF=3,AF=1,
∵∠AOB=90°,
∴∠BOC+∠OBC=∠BOC+∠AOF=90°,
∴∠BOC=∠AOF,
∵OA=OB,
∴△BOE≌△AOF(AAS),
∴BE=AF=1,OE=OF=3,
∴B(﹣1,3),
设直线AB的解析式为y=kx+b,
∴![]() ,
,
解得: ,
,
∴直线AB的解析式为y=﹣![]() x+
x+![]() ,
,
当x=0时,y=![]() ,
,
∴点C的坐标为(0,![]() ),
),
故答案为:(0,![]() ).
).

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目