题目内容
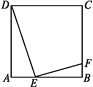
【题目】如图,四边形![]() 中,
中,![]() .动点
.动点![]() 从
从![]() 点出发,以
点出发,以![]() 的速度向
的速度向![]() 点移动,设移动的时间为
点移动,设移动的时间为![]() 秒.
秒.
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)在(1)的条件下,判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
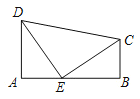
【答案】(1)当x=5时,点E在线段CD的垂直平分线上;(2)DE与CE的位置关系是DE⊥CE,理由见解析
【解析】
(1)根据垂直平分线的性质得出DE=CE,利用勾股定理得出![]() ,然后建立方程求解即可
,然后建立方程求解即可
(2)根据第(1)问的结果,易证△ADE≌△BEC,根据全等三角形的性质有∠ADE=∠CEB,再通过等量代换可得∠AED+∠CEB=90°,进而求出∠DEC=90°,则可说明DE⊥CE.
解:(1) ∵点E在线段CD的垂直平分线上,
∴DE=CE,
∵∠A=∠B= 90°
![]()
![]()
![]()
![]()
解得![]()
∴当x=5时,点E在线段CD的垂直平分线上
(2)DE与CE的位置关系是DE⊥CE;
理由是:当x=5时,AE=2×5cm=10cm=BC,
∵AB=25cm,DA=15cm,CB=10cm,
∴BE=AD=15cm,
在△ADE和△BEC中,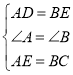
∴△ADE≌△BEC(SAS),
∴∠ADE=∠CEB,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°-(∠AED+∠CEB)=90°,
∴DE⊥CE.

练习册系列答案
相关题目