Question

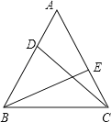
【题目】如图，在等边△ABC中，DE分别是边AB、AC上的点，且AD＝CE，则∠ADC+∠BEA＝（　　）

A.180°B.170°C.160°D.150°

Answer 1

【答案】A

【解析】

根据等边三角形的性质，得出各角相等各边相等，已知AD＝CE，利用SAS判定△ADC≌△CEB，从而得出∠ACD＝∠CBE，则∠BCD+∠CBE＝∠BCD+∠ACD＝∠ACB＝60°，进而利用四边形内角和解答即可．

∵△ABC是等边三角形，

∴∠A＝∠ACB＝60°，AC＝BC

∵AD＝CE

∴△ADC≌△CEB（SAS）

∴∠ACD＝∠CBE

∴∠BCD+∠CBE＝∠BCD+∠ACD＝∠ACB＝60°．

∴∠BOC＝120°，

∴∠DOE＝120°，

∴∠ADC+∠BEA＝360°﹣60°﹣120°＝180°，

故选：A．