题目内容
【题目】(1)如图1,P是∠ABC内一点,请过点P画射线PD,使PD∥BC;过点P画直线PE∥BA,交BC于点E.请画图并通过观察思考后你发现∠ABC与∠DPE的大小关系是 ,并说明理由.
(2)如图2,直线a,b所成的角跑到画板外面去了,为了测量这两条直线所成的角的度数,请画图并简单地写出你的方法.

【答案】(1)相等或互补 (2)见解析
【解析】试题分析:(1)分两种情况讨论;(2)利用平行线的性质或三角形的内角和设计方法.
试题解析:(1)相等或互补
理由如下:
如图1①,
DP交AB于点F.
∵PD∥BC,
∴∠ABC=∠AFP,
∵PE∥BA,
∴∠AFP=∠DPE,
∴∠ABC=∠DPE;
如图1②,
设DP交AB于点F.
∵PD∥BC,
∴∠ABC=∠CEP,
∵PD∥BC,
∴∠CEP+∠DPE=180°,
∴∠ABC+∠DPE=180°;
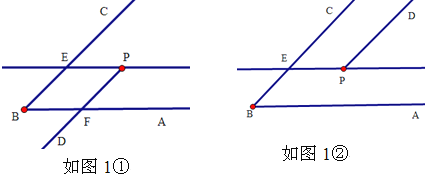
(2)方法一:
如图2①,设直线b与木板交于点P,
过点P作PC∥a,量出直线b与PC的夹角度数,即为直线a,b所成角的度数,
依据是:两直线平行,同位角相等;
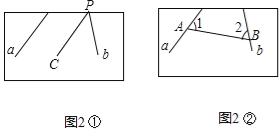
方法二:
如图2②,在直线a,b上各取一点A,B,
连结AB,测得∠1,∠2的度数,
则180°﹣∠1﹣∠2即为直线a,b所成角的度数;
依据是:三角形内角和为180°.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目