题目内容
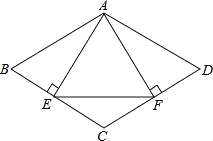
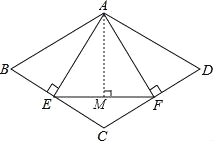
【题目】如图，菱形ABCD中，AB=4，∠B=60°，AE⊥BC，AF⊥CD，垂足分别为E，F，连接EF，则△AEF的面积是（ ）
A．4
B．3 C．2 D．
【答案】B
【解析】
试题分析：首先利用菱形的性质及等边三角形的判定可得判断出△AEF是等边三角形，再根据三角函数计算出AE=EF的值，再过A作AM⊥EF，再进一步利用三角函数计算出AM的值，即可算出三角形的面积．
∵四边形ABCD是菱形， ∴BC=CD，∠B=∠D=60°， ∵AE⊥BC，AF⊥CD，
∴BC×AE=CD×AF，∠BAE=∠DAF=30°， ∴AE=AF， ∵∠B=60°， ∴∠BAD=120°，
∴∠EAF=120°﹣30°﹣30°=60°， ∴△AEF是等边三角形， ∴AE=EF，∠AEF=60°，
∵AB=4， ∴BE=2， ∴AE=
=2
， ∴EF=AE=2
， 过A作AM⊥EF，
∴AM=AEsin60°=3， ∴△AEF的面积是：
EFAM=
×2×3=3．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
