题目内容
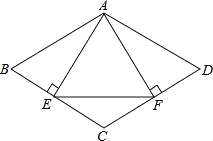
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .
【答案】![]()
【解析】试题分析:延长AB至M,使BM=AE,连接FM,证出△DAE≌EMF,得到△BMF是等边三角形,再利用菱形的边长为4求出时间t的值.延长AB至M,使BM=AE,连接FM, ∵四边形ABCD是菱形,∠ADC=120°
∴AB=AD,∠A=60°, ∵BM=AE, ∴AD=ME, ∵△DEF为等边三角形,
∴∠DAE=∠DFE=60°,DE=EF=FD, ∴∠MEF+∠DEA═120°,∠ADE+∠DEA=180°﹣∠A=120°,
∴∠MEF=∠ADE, ∴△DAE≌EMF(SAS),∴AE=MF,∠M=∠A=60°, 又∵BM=AE,
∴△BMF是等边三角形, ∴BF=AE, ∵AE=t,CF=2t, ∴BC=CF+BF=2t+t=3t, ∵BC=4,
∴3t=4, ∴t=![]()

练习册系列答案
相关题目