��Ŀ����
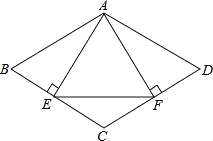
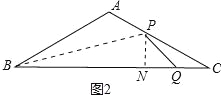
����Ŀ����ͼ1������ABC�У���A=120�㣬AB=AC����P��Qͬʱ�ӵ�B����������ͬ���ٶȷֱ�������B��A��C������BC�˶�������PQ������P�����Cʱ����P��Qͬʱֹͣ�˶�����BQ=x����BPQ����ABC�ص����ֵ����ΪS����ͼ2��S����x�ĺ���ͼ������0��x��8��8��x��m��m��x��16ʱ�������Ľ���ʽ��ͬ����
��1����գ�m��ֵΪ ��
��2����S����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��3����ֱ��д����PCQΪ����������ʱx��ֵ��

���𰸡�(1)![]() ��(2)��0��m��8ʱ��s =
��(2)��0��m��8ʱ��s =![]() ����
����![]() ��x��16ʱ��s=
��x��16ʱ��s=![]() +4x����
+4x����![]() ��x��16ʱ��s=
��x��16ʱ��s=![]() ��(3)
��(3)![]() +4��8+
+4��8+![]() ��
��
��������
�����������1�������������BC�ij����ɣ�
��2��������������0��m��8����![]() ��x��16����
��x��16����![]() ��x��16���ֱ������APQ������ɣ�
��x��16���ֱ������APQ������ɣ�
��3������������������������P��AB�ϣ���Q��BC�ϣ���PQC������Ϊ���������Σ�������P��AC�ϣ���Q��BC�ϣ�����PQ=QC�г����̼���.������P��AC�ϣ���Q��BC���ӳ��ߣ�����CP=CQ�г����̼��ɣ�
�����������1����ͼ1�У���AM��BC��PN��BC������ֱ�ΪM��N��
������AB=AC=8����A=120�㣬
���BAM=��CAM=60�㣬��B=��C=30�㣬
��AM=![]() AB=4��BM=CM=
AB=4��BM=CM=![]() ��
��
��BC=![]() ��
��
��m=BC=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2������0��m��8ʱ����ͼ1�У�
��RT��PBN�У��ߡ�PNB=90�㣬��B=30�㣬PB=x��
��PN=![]() x��
x��
s=![]() BQPN=
BQPN=![]() x
x![]() x=
x=![]() ��
��
����![]() ��x��16ʱ����ͼ2�У�
��x��16ʱ����ͼ2�У�
��RT��PBN�У�span>��PC=16��x����PNC=90�㣬��C=30�㣬
��PN=![]() PC=8��
PC=8��![]() x��
x��
��s=![]() BQPN=
BQPN=![]() x��8��
x��8��![]() x��=
x��=![]() +4x��
+4x��
����![]() ��x��16ʱ��
��x��16ʱ��
s=![]() ��
��![]() ��8��
��8��![]() x��=
x��=![]() ��
��
���ϣ���0��m��8ʱ��s =![]() ����
����![]() ��x��16ʱ��s=
��x��16ʱ��s=![]() +4x����
+4x����![]() ��x��16ʱ��s=
��x��16ʱ��s=![]() .
.
��3��������P��AB�ϣ���Q��BC��ʱ����PQC�������ǵ��������Σ�
������P��AC�ϣ���Q��BC��ʱ��PQ=QC��
��PC=![]() QC��
QC��
��16��x=![]() ��
��![]() ��x����
��x����
��x=![]() +4��
+4��
������P��AC�ϣ���Q��BC���ӳ���ʱ��PC=CQ��
��16��x=x��![]() ��
��
��x=8+![]() ��
��
���PCQΪ����������ʱx��ֵΪ![]() +4��8+
+4��8+![]() ��
��


 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�