题目内容
【题目】已知,数轴上有两点A、B对应的数分别为1,5,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、B的距离相等,求点A、B的距离及x的值.
(2)数轴上是否存在点P,使得点P到点A、B的距离之和最小?若存在,请求出最小值;并求出取得最小值时x可以取的整数值;若不存在,说明理由.
(3)点A、B分别以3个单位长度/秒,2个单位长度/秒的速度向右运动,同时点P以4个单位长度/秒的速度从O点向左运动,当遇到A时,点P立即以不变的速度向右运动,当遇到B时,点P立即以不变的速度向左运动,并不停往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?
【答案】(1)1,5,2;(2)存在,最小值为6,x可以取的整数值有1、0、1、2、3、4、5;(3)48
【解析】
(1)根据数轴上的两点距离公式和中点公式列式求解即可;
(2)分类讨论点P分别在点A左侧、点A、点B之间、点B右侧时分别求出,进行比较即可求出最小值;
(3)设经过t分钟点A与点B重合,根据点A比点B运动的距离多6,列出方程,求出t的值,即为点P的运动时间,再乘以点P运动的速度,即可得点P所经过的总路程.
解:(1)∵点A、B对应的数分别为1,5,
∴![]() ,即点A、B的距离为6;
,即点A、B的距离为6;
∵点P到点A、B的距离相等,则P为AB中点,
则有:![]() ,所以
,所以![]() ;
;
(2)数轴上存在点P,使得点P到点A、B的距离之和最小,
当点P在点A左侧时,点P到点A、B的距离之和为:PA+PB=2PA+AB=2PA+6,
当点P在点A、点B之间时,点P到点A、B的距离之和为:PA+PB=AB=6,
当点P在点B右侧时,点P到点A、B的距离之和为:PA+PB=2PB+AB=2PA+6,
所以当点P在点A、点B之间时(含点A、点B),点P到点A、B的距离之和最小,最小值为6,
点A、点B之间的整数值有1、0、1、2、3、4、5,即为x可以取的整数值;
(3)设经过t分钟点A与点B重合,依题意得:
1+3t=5+2t+6,解得:t=12,
所以4t=4×12=48,
所以点P所经过的总路程是48个单位长度.

 阅读快车系列答案
阅读快车系列答案【题目】某次试验中,测得两个变量v和m的对应数据如下表,则v和m之间的关系最接近下列函数中的( )
m | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
v | ﹣6.10 | ﹣2.90 | ﹣2.01 | ﹣1.51 | ﹣1.19 | ﹣1.05 | ﹣0.86 |
A. v=m2﹣2 B. v=﹣6m C. v=﹣3m﹣1 D. v=![]()
【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表(单位:分):
项目人员 | 阅读能力 | 思维能力 | 表达能力 |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将能被录用?
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
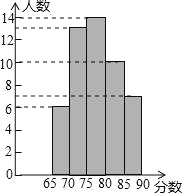
(3)公司按照(2)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.