题目内容
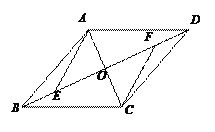
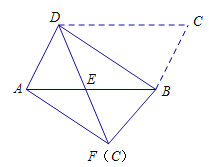
【题目】如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
(1)求证:![]() ;
;
(2)判断AF与BD是否平行,并说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据折叠的性质可证∠CDB =∠EDB,由平行四边形的性质,可证∠CDB =∠EBD,等量代换可证得结论;
(2)根据(1)结论可知DE=BE,然后由平行四边形的对边相等和等量代换,可知AE=EF,从而根据等边对等角可得∠EAF=∠EFA,再由三角形的内角和得出∠EDB= ∠EFA,因此可证得AF∥BD(或由AB与BD互相平分证得四边形ADBF是平行四边形).
(1)由折叠可知:∠CDB =∠EDB
∵四边形ABCD是平行四边形
∴DC∥AB
∴∠CDB =∠EBD
∴∠EDB=∠EBD
(2)∵∠EDB=∠EBD
∴DE=BE
由折叠可知:DC=DF
∵四边形ABCD是平行四边形
∴DC=AB
∴AE=EF
∴∠EAF=∠EFA
△BED中,∠EDB+∠EBD+∠DEB=180°
即2∠EDB+∠DEB=180°
同理△AEF中,2∠EFA+∠AEF=180°
∵∠DEB=∠AEF
∴∠EDB= ∠EFA
∴AF∥BD

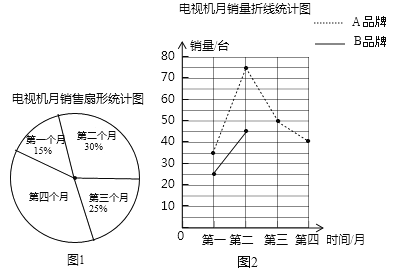
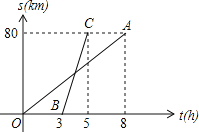
【题目】2014年全国两会民生话题成为社会焦点.合肥市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了合肥市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.
组别 | 焦点话题 | 频数(人数) |
A | 食品安全 | 80 |
B | 教育医疗 | m |
C | 就业养老 | n |
D | 生态环保 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= .扇形统计图中E组所占的百分比为 %;
(2)合肥市人口现有750万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?