题目内容
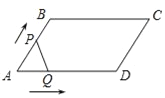
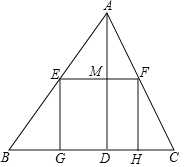
【题目】
是一块锐角三角形材料，边
，高
，要把它加工成矩形零件EFHG，使矩形的一边GH在BC上，其余两个顶点E、F在AB、AC上，
求证：EF：
：AD；
设
，
，用含x的代数式表示y；
设矩形EFHG的面积是S，求S与x的函数关系式，并求当x为何值时S取得最大值，最大值为多少？
【答案】（1）见解析 （2）
（3）
【解析】分析：（1）根据EF∥BC，得出△AEF∽△ABC，进而得出EF：BC=AM：AD；
（2）设EF=x，EG=y，利用相似三角形的性质用x表示出y即可；
（3）根据矩形面积公式求出S与x之间的解析式，即可得出结论．
详解：
证明：
四边形EFHG是矩形，
，
∽
，
；
解：设
，
，
故
，
解得：．
．
即
．
当
时，矩形EGHF的面积最大
最大值．
练习册系列答案
相关题目
