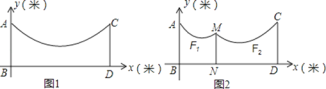��Ŀ����
����Ŀ��ij�̵�����һ����Ʒ��ÿ���ɱ�8Ԫ���涨ÿ����Ʒ�ۼ۲����ڳɱ����Ҳ�����20Ԫ�����г�����ÿ���������y��������ÿ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ���� | 10 | 11 | 12 | 13 | 14 | x |
������y������ | 100 | 90 | 80 | 70 | �� �� | �� �� |
��1��������ı������������
��2�������Ʒÿ���������ΪwԪ����w��x֮��ĺ�������ʽ��
��3�����㣨2�����ۼ�Ϊ����Ԫʱ��������������������Ƕ��٣�
���𰸡���1������������2��w����10x2+280x��1600����3���ۼ�Ϊ14Ԫʱ���������������������360Ԫ��
��������
��1����y=kx+b���ɴ���ϵ�������г������飺![]() ����ã�
����ã�![]()
��y=��10x+200����x=14ʱ��y=60.��2��������ã�w��x֮��ĺ�������ʽΪ��w����x��8������10x+200������10x2+280x��1600����3����w����10x2+280x��1600����10��x��14��2+360�����ۼ�Ϊ14Ԫʱ���������������������360Ԫ��
�⣺��1����������y��������ÿ���ۼ�x��Ԫ������һ�κ�����ϵΪy��kx+b��
��![]() ��
��
��ã�![]() ��
��
��������y��������ÿ���ۼ�x��Ԫ������һ�κ�����ϵΪy����10x+200��
��x��14ʱ��y��60��
�ʴ�Ϊ��60����10x+200��
��2��������ã�w��x֮��ĺ�������ʽΪ��w����x��8������10x+200������10x2+280x��1600��
��3����w����10x2+280x��1600����10��x��14��2+360��
���ۼ�Ϊ14Ԫʱ���������������������360Ԫ��

����Ŀ�����Ϲ��ʻ�ѩ�Խ�������������������ѩ�����ߣ�һ��ѩ�ߴ�ɽ�»��£���û��о���y����λ��m���뻬��ʱ��x����λ��s��֮��Ĺ�ϵ���Խ��Ƶ��ö��κ�������ʾ��
����ʱ��x/s | 0 | 1 | 2 | 3 | �� |
�����y/m | 0 | 4 | 12 | 24 | �� |
��1�����ݱ�������������κ����ı���ʽ���ֲ�������ѩ�ߵij��������յ�ľ����Լ840m������Ҫ����ʱ����ܵ����յ㣿
��2�����õ��Ķ��κ���ͼ������������ƽ��2����λ��������ƽ��5����λ����ƽ�ƺ�ĺ�������ʽ��