Question

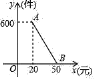
【题目】某网商经销一种畅销玩具，每件进价为18元，每月销量y（件）与销售单价x（元）之间的函数关系如图中线段AB所示．

（1）当销售单价为多少元时，该网商每月经销这种玩具能够获得最大销售利润？最大销售利润是多少？（销售利润=售价﹣进价）

（2）如果该网商要获得每月不低于3500元的销售利润．那么至少要准备多少资金进货这种玩具？

Answer 1

【答案】(1) 当销售单价为34元时，该网商每月经销这种玩具能够获得最大销售利润，最大销售利润是5120元；(2) 该网商要获得每月不低于3500元的销售利润．那么至少要准备2520元进货这种玩具．

【解析】

（1）先用待定系数法求出AB段对应的函数解析式，然后根据 “每月的利润等于每件产品的利润乘以每月销售量”即可计算出每件产品的利润；

（2）先根据该网商要获得每月不低于3500元的销售利润，列不等式求出x的取值范围，设准备资金为m元，列出一次函数关系式求解即可.

解：（1）设AB段对应的函数解析式为y=kx+b，

，得，

即AB段对应的函数解析式为y=﹣20x+1000，

设销售利润为w元，

w=（x﹣18）（﹣20x+1000）=﹣20x2+1360x﹣18000=﹣20（x﹣34）2+5120，∵20≤x≤50，

∴当x=34时，w取得最大值，此时w=5120，

答：当销售单价为34元时，该网商每月经销这种玩具能够获得最大销售利润，最大销售利润是5120元；

（2）∵该网商要获得每月不低于3500元的销售利润，

∴﹣20（x﹣34）2+5120≥3500，

解得，25≤x≤43，

设准备资金为m元，

则m=18（﹣20x+1000）=﹣360x+18000，

∴当x=43时，m取的最小是，此时m=2520，

答：该网商要获得每月不低于3500元的销售利润．那么至少要准备2520元进货这种玩具．