Question

【题目】如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点D在AB上，以BD为直径的⊙O切AC于点E，连接DE并延长，交BC的延长线于点F．

（1）求证：△BDF是等边三角形；

（2）连接AF、DC，若BC＝3，写出求四边形AFCD面积的思路．

Answer 1

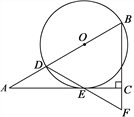
【答案】（1）证明见解析；（2）思路见解析.

【解析】试题分析：(1)连接OE，因AC切⊙O于点E，根据切线的性质可得∠OEA=90° ；再由∠A=30°，∠ACB=90°，根据三角形的内角和定理可得∠AOE=60°，∠B=60°因OD=OE，可得∠ODE=∠OED=60°，所以∠F=∠B=∠ODE，即可判断△BDF是等边三角形 ；（2）如图，作DH⊥AC于点H，求四边形AFCD的面积思路有以下几步：①由∠ACB=90°，∠BAC=30°，BC=3,可求AB，AC的长；②由∠AEO=90°，∠OAE=30°,可知AO=2OE，可求AD，DB，DH的长； ③由（1）可知BF=BD，可求CF的长； ④由AC，DH，CF的长可求四边形AFCD的面积.

试题解析：

（1）证明：连接OE．

∵AC切⊙O于点E，

∴．

∵， ,

∴, .

∵，

∴．

∴．

∴△BDF是等边三角形．

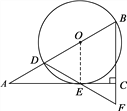
（2）如图，作DH⊥AC于点H.

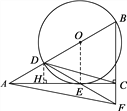
①由∠ACB=90°，∠BAC=30°，BC=3,可求AB，AC的长；

②由∠AEO=90°，∠OAE=30°,可知AO=2OE，可求AD，DB，DH的长；

③由（1）可知BF=BD，可求CF的长；

④由AC，DH，CF的长可求四边形AFCD的面积.