题目内容
【题目】如图，在平面直角坐标系中，点A，B坐标分别为A（0，a），B（b，a），且实数a，b满足（a﹣3）2+|b﹣5|=0，现同时将点A，B分别向下平移3个单位，再向左平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，AB．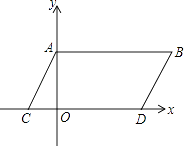 
（1）求点C，D的坐标及四边形ABDC的面积；
（2）在y轴上是否存在一点M，连接MC，MD，使S△MCD=S四边形ABDC？若存在这样一点，求出点M的坐标；若不存在，试说明理由．
【答案】
（1）解：∵（a﹣3）2+|b﹣5|=0，
∴a=3，b=5，
∴点A（0，3），B（5，3）．
将点A，B分别向下平移3个单位，再向左平移1个单位，得到点C、D，
∴点C（﹣1，0），D（4，0）．
由AB平移得出CD可知，AB∥CD，且AB=CD=5，
∴四边形ABDC为平行四边形，
∴S四边形ABDC=5×3=15．
（2）解：设存在点M（0，y），
根据题意得：S△MCD= 
×5|y|=S四边形ABDC=15，
∴ ×5|y|=15，解得：y=±6，
∴存在点M（0，6）或（0，﹣6），使S△MCD=S四边形ABDC．
【解析】（1）由偶次方及绝对值的非负性可求出a、b的值，进而即可得出点A、B的坐标，再根据平移的性质可得出点C、D的坐标以及四边形ABDC为平行四边形，套用平行四边形的面积公式即可求出四边形ABDC的面积；（2）设存在点M（0，y），根据三角形的面积结合S△MCD=S四边形ABDC ， 即可得出关于y的含绝对值符号的一元一次方程，解之即可得出结论．
【考点精析】本题主要考查了三角形的面积的相关知识点，需要掌握三角形的面积=1/2×底×高才能正确解答此题．
练习册系列答案
相关题目
