题目内容
【题目】如图:在等边三角形ABC中,点E在线段AB上,点D在CB的延长线上,且AE=BD,试确定线段DE与EC的大小关系,并说明理由. 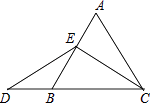
【答案】解:DE=EC
理由:如图,过E作EF∥BC,交AC于F
∵△ABC是等边三角形
∴AB=AC,∠A=∠ABC=∠ACB=60°
∵EF∥BC
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°
∴△AEF是等边三角形
∴AE=AF=EF
∵AE=BD,AB=AC
∴BD=EF,BE=CF
∵∠ABC=∠AFE=60°
∴∠EBD=∠EFC=120°
∴△BDE≌△FEC(SAS)
∴DE=EC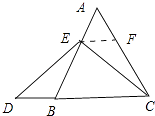
【解析】先过E作EF∥BC,交AC于F,构造等边三角形AEF,再根据SAS判定△BDE≌△FEC,即可得出结论.
【考点精析】通过灵活运用等边三角形的性质,掌握等边三角形的三个角都相等并且每个角都是60°即可以解答此题.

练习册系列答案
相关题目