题目内容
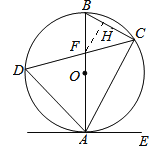
【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,作直线AE,且∠EAC=∠D.
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD=![]() ,CF=
,CF=![]() ,求BF的长.
,求BF的长.

【答案】(1)见解析;(2)3.
【解析】
试题(1)、根据直径所对的圆周角为直角得出∠BCA=90°,从而得出∠B+∠BAC=90°,根据∠B=∠D,∠EAC=∠D得出∠B=∠EAC,从而利用等量代换得出∠BAE=90°,得出切线;(2)、过点F作FH⊥BC于点H,根据同弧所对的圆周角相等得出∠BAD=∠BCD,根据CF的长度求出CH的长度,然后求出BH的长度,然后根据∠B=60°以及Rt△BFH的三角函数求出BF的长度.
试题解析:解:(1)证明:∵AB是⊙O的直径, ∴∠BCA=90°, ∴∠B+∠BAC=90°,
∵∠D=∠B,∠EAC=∠D, ∴∠EAC=∠B,∴∠EAC+∠BAC=90°,即∠BAE=90°,
∴BA⊥AE, ∵BA过O, ∴直线AE是⊙O的切线.
(2)解:如图,作FH⊥BC于点H,
∵∠BAD=∠BCD,cos∠BAD=![]() , ∴cos∠BCD =
, ∴cos∠BCD =![]() ,
,
在Rt△CFH中,∵CF=![]() ∴CH=CF·cos∠BCD=
∴CH=CF·cos∠BCD=![]() ×
×![]() =
=![]() ,
,
∵BC=4, ∴BH=BC-CH=4-![]() =
=![]() ,
,
∵AB是⊙O的直径, ∴∠BCA=90°, ∵∠BAC=30°, ∴∠B=60°,
∴BF=![]() =
=![]() =3.
=3.

练习册系列答案
相关题目