题目内容
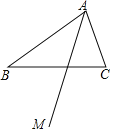
【题目】如图,在△ABC中,射线AM平分∠BAC.
(1)尺规作图(不写作法,保留作图痕迹)作BC的中垂线,与AM相交于点G,连接BG、CG;
(2)在(1)条件下,∠BAC和∠BGC有何数量关系?并证明你的结论.
【答案】(1)详见解析;(2)∠BAC+∠BGC=180°,证明详见解析.
【解析】
(1)作线段BC的垂直平分线即可;
(2)在AB上截取AD=AC,连接DG.首先证明△DAG≌△CAG(SAS),推出∠ABG+∠ACG=180°,利用四边形内角和定理即可解决问题.
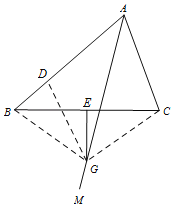
解:(1)线段BC的中垂线EG如图所示:
(2)结论:∠BAC+∠BGC=180°.
理由:在AB上截取AD=AC,连接DG.
∵AM平分∠BAC,
∴∠DAG=∠CAG,
在△DAG和△CAG中
∵
∴△DAG≌△CAG(SAS),
∴∠ADG=∠ACG,DG=CG,
∵G在BC的垂直平分线上,
∴BG=CG,
∴BG=DG,
∴∠ABG=∠BDG,
∵∠BDG+∠ADG=180°,
∴∠ABG+∠ACG=180°,
∵∠ABG+∠BGC+∠ACG+∠BAC=360°,
∴∠BAC+∠BGC=180°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目