ЬтФПФкШн
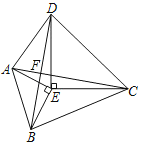
ЁОЬтФПЁПЖЈвхЃКШчЭМ1ЃЌЕуMЃЌNАбЯпЖЮABЗжИюГЩAMЃЌMNКЭBNЃЌШєвдAMЃЌMNЃЌBNЮЊБпЕФШ§НЧаЮЪЧвЛИіжБНЧШ§НЧаЮЃЌдђГЦЕуMЃЌNЪЧЯпЖЮABЕФЙДЙЩЗжИюЕуЃЎ

ЃЈ1ЃЉвбжЊЕуMЃЌNЪЧЯпЖЮABЕФЙДЙЩЗжИюЕуЃЌШєAM=2ЃЌMN=3ЃЌдђBN=________ЃЛ
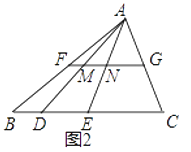
ЃЈ2ЃЉШчЭМ2ЃЌдкЁїABCжаЃЌFGЪЧжаЮЛЯпЃЌЕуDЃЌEЪЧЯпЖЮBCЕФЙДЙЩЗжИюЕуЃЌЧвECЃОDEЁнBDЃЌСЌНгADЃЌAEЗжБ№НЛFGгкЕуMЃЌNЃЌЧѓжЄЃКЕуMЃЌNЪЧЯпЖЮFGЕФЙДЙЩЗжИюЕуЃЛ
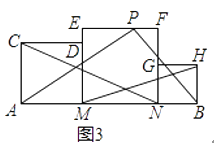
ЃЈ3ЃЉШчЭМ3ЃЌвбжЊЕуMЃЌNЪЧЯпЖЮABЕФЙДЙЩЗжИюЕуЃЌMNЃОAMЁнBNЃЌЫФБпаЮAMDCЃЌЫФБпаЮMNFEКЭЫФБпаЮNBHGОљЪЧе§ЗНаЮЃЌЕуPдкБпEFЩЯЃЌЪдЬНОПSЁїACN ЃЌSЁїAPB ЃЌSЁїMBHЕФЪ§СПЙиЯЕЃЎ
SЁїACN=________ЃЛSЁїMBH=________ЃЛSЁїAPB=________ЃЛSЁїACN ЃЌSЁїAPBЃЌSЁїMBHЕФЪ§СПЙиЯЕЪЧ________ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉМћНтЮі.
ЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉМћНтЮі.
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЗжРрЬжТл:ЕБMNЮЊзюДѓЯпЖЮЪБ;ЕБBNЮЊзюДѓЯпЖЮЪБ;МДвбжЊЕФСНЬѕЯпЖЮжаНЯГЄЕФЯпЖЮMNПЩФмЮЊаББпЛђЫљЧѓЕФBNвВПЩФмЮЊаББпЃЛ
ЃЈ2ЃЉгЩвбжЊЁАFGЪЧжаЮЛЯпЁБЕУBD=2FMЃЌDE=2MNЃЌEC=2NGЃЌгЩDЃЌEЪЧЯпЖЮBCЕФЙДЙЩЗжИюЕуЃЌЧвECЃОDEЃОBDЕУГіEC2=DE2+DB2ЃЌдйЗжБ№ДњЛЛЮЊ2NGЁЂ2MNЁЂ2FMЃЌдМШЅЯЕЪ§4ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉгЩШ§НЧаЮУцЛ§ЙЋЪНЃЌЗжБ№БэЪОГіSЁїACNЁЂSЁїMBHЁЂSЁїPABЃЌЙлВь3ИіЪНзгжаЃЌГіЯжЕФAM2ЁЂBN2 ЁЂMN2ЃЌПЩЕУSЁїAPB=SЁїACN+SЁїMBH.
ЪдЬтНтЮіЃКЃЈ1ЃЉЗжСНжжЧщПіЃК
ЂйЕБMNЮЊзюДѓЯпЖЮЪБЃЌ
ЁпЕу MЁЂNЪЧЯпЖЮABЕФЙДЙЩЗжИюЕуЃЌ
ЁрBN=![]() ЃЛ
ЃЛ
ЂкЕБBNЮЊзюДѓЯпЖЮЪБЃЌ
ЁпЕуMЁЂNЪЧЯпЖЮABЕФЙДЙЩЗжИюЕуЃЌ
ЁрBN=![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃКBNЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЁпЕуFЁЂMЁЂNЁЂGЗжБ№ЪЧABЁЂADЁЂAEЁЂACБпЩЯЕФжаЕуЃЌ
ЁрFMЁЂMNЁЂNGЗжБ№ЪЧЁїABDЁЂЁїADEЁЂЁїAECЕФжаЮЛЯпЃЌ
ЁрBD=2FMЃЌDE=2MNЃЌEC=2NGЃЌ
ЁпЕуDЃЌEЪЧЯпЖЮBCЕФЙДЙЩЗжИюЕуЃЌЧвECЃОDEЃОBDЃЌ
ЁрEC2=DE2+DB2 ,
Ёр4NG2=4MN2+4FM2 ,
ЁрNG2=MN2+FM2 ,
ЁрЕуMЃЌNЪЧЯпЖЮFGЕФЙДЙЩЗжИюЕуЃЛ
ЂЧЁпЫФБпаЮAMDCЃЌЫФБпаЮMNFEКЭЫФБпаЮNBHGОљЪЧе§ЗНаЮЃЌ
ЁрSЁїACN= ![]() ЃЈAM+MNЃЉAC=
ЃЈAM+MNЃЉAC= ![]() ЃЈAM+MNЃЉAM=
ЃЈAM+MNЃЉAM= ![]() AM2+
AM2+ ![]() MNAMЃЌ
MNAMЃЌ
SЁїMBH= ![]() ЃЈMN+BNЃЉBH=
ЃЈMN+BNЃЉBH= ![]() ЃЈMN+BNЃЉBN=
ЃЈMN+BNЃЉBN= ![]() BN2+
BN2+ ![]() MNBNЃЌ
MNBNЃЌ
SЁїPAB= ![]() ЃЈAM+NM+BNЃЉFN=
ЃЈAM+NM+BNЃЉFN= ![]() ЃЈAM+MN+BNЃЉMN=
ЃЈAM+MN+BNЃЉMN= ![]() MN2+ /span>
MN2+ /span>![]() MNAM+
MNAM+ ![]() MNBNЃЌ
MNBNЃЌ
ЁрSЁїAPB=SЁїACN+SЁїMBH ЃЌ
ЙЪД№АИЮЊSЁїAPB=SЁїACN+SЁїMBH ЃЎ