题目内容
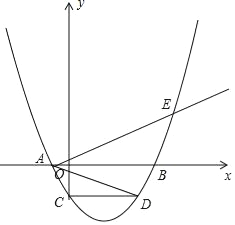
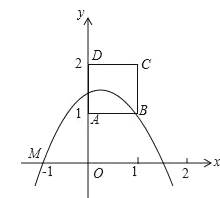
【题目】如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(﹣1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
A. ﹣2≤a≤﹣1 B. ﹣2≤a≤﹣![]() C. ﹣1≤a≤﹣
C. ﹣1≤a≤﹣![]() D. ﹣1≤a≤﹣
D. ﹣1≤a≤﹣![]()
【答案】C
【解析】
当顶点与A点重合,可以知道顶点坐标为(0,1)且抛物线过(-1,0),由此可求出a;当顶点与C点重合,顶点坐标为(1,2)且抛物线过(-1,0),由此也可求a,然后由此可判断a的取值范围.
解:∵顶点是矩形ABCD上(包括边界和内部)的一个动点,
∴当顶点与A点重合,顶点坐标为(0,1),则抛物线解析式y=ax2+1,
∵抛物线过M(-1,0),
∴0=a+1,解得a=-1,
当顶点与C点重合,顶点坐标为(1,2),则抛物线解析式y=a(x-1)2+2,
∵抛物线过M(-1,0),
∴0=4a+2,解得a=-12
∵顶点可以在矩形内部,
∴-1≤a≤-12.
故选C.

练习册系列答案
相关题目