ЬтФПФкШн
ЁОЬтФПЁПЬНОПгыЗЂЯжЃКШчЭМЃЈ1ЃЉЫљЪОЕФЭМаЮЃЌЯёЮвУЧГЃМћЕФбЇЯАгУЦЗвЛдВЙцЃЌЮвУЧЃЌВЛЗСАбетбљЭМаЮНазіЁАЙцаЮЭМ
ЃЈ1ЃЉЙлВьЁАЙцаЮЭМЃЈ1ЃЉЁБЃЌЪдЬНОПЁЯBDCгыЁЯAЁЂЁЯBЁЂЁЯCжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧыФужБНгРћгУвдЩЯНсТлЃЌНтОівдЯТЮЪЬтЃК
ЂйШчЭМЃЈ2ЃЉЃЌАбвЛПщШ§НЧГпXYZЗХжУдкЁїABCЩЯЪЙШ§НЧГпЕФСНЬѕжБНЧБпXYЁЂXZЧЁКУОЙ§ЕуBЁЂCЃЌШєЁЯAЃН40ЁуЃЌдђЁЯABX+ЁЯACXЃНЁЁ ЁЁЁуЃЎ
ЂкШчЭМЃЈ3ЃЉЃЌDCЦНЗжЁЯADBЃЌECЦНЗжЁЯAEBЃЌШєЁЯDAEЃН40ЁуЃЌЁЯDBEЃН130ЁуЃЌЧѓЁЯDCEЕФЖШЪ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉЁЯBDCЃНЁЯBAC+ЁЯB+ЁЯCЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉЂй50ЃЛЂкЁЯDCEЃН85ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШСЌНгADВЂбгГЄжСЕуFЃЌШЛКѓИљОнЭтНЧЕФаджЪЃЌМДПЩХаЖЯГіЁЯBDCЃНЁЯBAC+ЁЯB+ЁЯCЃЛ
ЃЈ2ЃЉЂйгЩЃЈ1ЃЉПЩЕУЁЯA+ЁЯABX+ЁЯACXЃНЁЯXЃЌШЛКѓИљОнЁЯAЃН40ЁуЃЌЁЯXЃН90ЁуЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉЂкгЩЁЯAЃН40ЁуЃЌЁЯDBEЃН130ЁуЃЌЧѓГіЁЯADE+ЁЯAEBЕФжЕЃЌШЛКѓИљОнЁЯDCEЃНЁЯA+ЁЯADC+ЁЯAECЃЌЧѓГіЁЯDCEЕФЖШЪ§МДПЩ.
ЃЈ1ЃЉШчЭМЃЌЁЯBDCЃНЁЯBAC+ЁЯB+ЁЯCЃЌРэгЩЪЧЃК
Й§ЕуAЁЂDзїЩфЯпAFЃЌ
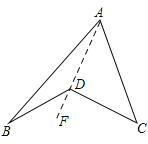
ЁпЁЯFDCЃНЁЯDAC+ЁЯCЃЌЁЯBDFЃНЁЯB+ЁЯBADЃЌ
ЁрЁЯFDC+ЁЯBDFЃНЁЯDAC+ЁЯBAD+ЁЯC+ЁЯBЃЌ
МДЁЯBDCЃНЁЯBAC+ЁЯB+ЁЯCЃЛ
ЃЈ2ЃЉЂйШчЭМЃЈ2ЃЉЃЌЁпЁЯXЃН90ЁуЃЌ
гЩЃЈ1ЃЉжЊЃКЁЯA+ЁЯABX+ЁЯACXЃНЁЯXЃН90ЁуЃЌ
ЁпЁЯAЃН40ЁуЃЌ
ЁрЁЯABX+ЁЯACXЃН50ЁуЃЌ
ЙЪД№АИЮЊЃК50ЃЛ
ЂкШчЭМЃЈ3ЃЉЃЌЁпЁЯAЃН40ЁуЃЌЁЯDBEЃН130ЁуЃЌ
ЁрЁЯADE+ЁЯAEBЃН130ЁуЉ40ЁуЃН90ЁуЃЌ
ЁпDCЦНЗжЁЯADBЃЌECЦНЗжЁЯAEBЃЌ
ЁрЁЯADCЃН![]() ЁЯADBЃЌЁЯAECЃН
ЁЯADBЃЌЁЯAECЃН![]() ЁЯAEBЃЌ
ЁЯAEBЃЌ
ЁрЁЯADC+ЁЯAECЃН![]() ЃН45ЁуЃЌ
ЃН45ЁуЃЌ
ЁрЁЯDCEЃНЁЯA+ЁЯADC+ЁЯAECЃН40Ёу+45ЁуЃН85ЁуЃЎ








