题目内容
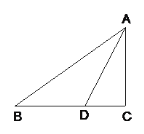
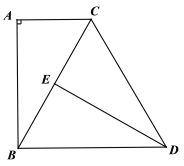
【题目】如图,在等边三角形ABC中,点D、E分别是边AC、BC上两点.将△ABC沿DE翻折,点C正好落在线段AB上的点F处,使得AF:BF=2:3.若BE=16,则点F到BC边的距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
作EM⊥AB于M,作FG⊥BC于G,由等边三角形的性质和直角三角形的性质求出BM=![]() BE=8,ME=
BE=8,ME=![]() BM=
BM=![]() ,由折叠的性质得出FE=CE,设FE=CE=x,则AB=BC=16+x,得出BF=
,由折叠的性质得出FE=CE,设FE=CE=x,则AB=BC=16+x,得出BF=![]() ,求出FM=BF-BM=
,求出FM=BF-BM=![]() ,在Rt△EFM中,由勾股定理得出方程,求出CE,进而得到BF的长,然后利用面积相等,即可求出FG的长.
,在Rt△EFM中,由勾股定理得出方程,求出CE,进而得到BF的长,然后利用面积相等,即可求出FG的长.
解:作EM⊥AB于M,作FG⊥BC于G,如图所示:
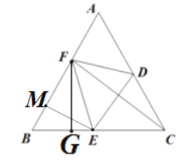
∵△ABC是等边三角形,
∴BC=AB,∠B=60°,
∵EM⊥AB,
∴∠BEM=30°,
∴BM=![]() BE=8,ME=
BE=8,ME=![]() BM=
BM=![]() ,
,
由折叠的性质得:FE=CE,设FE=CE=x,
则AB=BC=16+x,
∵AF:BF=2:3,
∴BF=![]() ,
,
∴FM=BF![]() BM=
BM=![]() ,
,
在Rt△EFM中,由勾股定理得:(![]() )2+(
)2+(![]() )2=x2,
)2=x2,
解得:x=19,或x=-16(舍去),
∴CE=19,BF=![]() ;
;
在△BEF中,有
![]() ,
,
∴![]() ,
,
即点F到BC的距离为![]() ;
;
故选择:D.

【题目】甲、乙两位同学5次数学选拔赛的成绩统计如下表,他们5次考试的总成绩相同,请同学们完成下列问题:
第1 次 | 第2 次 | 第 3次 | 第 4次 | 第5 次 | |
甲成绩 | 90 | 40 | 70 | 40 | 60 |
乙成绩 | 70 | 50 | 70 |
| 70 |
(1)统计表中,求![]() 的值,甲同学成绩的极差为多少;
的值,甲同学成绩的极差为多少;
(2)小颖计算了甲同学的成绩平均数为60,方差是![]() [(90﹣60)2+(40﹣60)2+(70﹣60)2+(40﹣60)2+(60﹣60)2]=360.
[(90﹣60)2+(40﹣60)2+(70﹣60)2+(40﹣60)2+(60﹣60)2]=360.
请你求出乙同学成绩的平均数和方差;
(3)从平均数和方差的角度分析,甲乙两位同学谁的成绩更稳定.
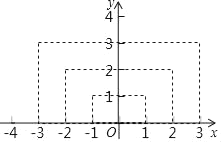
【题目】已知y是x的函数,x的取值范围为任意实数,如图是x与y的几组对应值,小华同学根据研究函数的己有经验探素这个函数的有关性质,并完成下列问题.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 2 | 1 | 0 | 1 | 2 | 3 | … |
(1)如图,小华在平面直角坐标系中描出了上述几组值对应的点,请你根据描出的点画出函数的图象;
(2)请根据你画出的函数图象,完成
①当x=﹣4时,求y的值;
②当2012≤|y|≤2019时,求x的取值范围.