Question

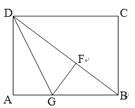
【题目】如图，四边形ABCD为⊙O的内接四边形，且对角线AC为直径，AD=BC，过点D作DG⊥AC，垂足为E，DG分别与AB及CB延长线交于点F、M．

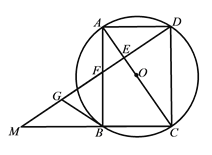
（1）求证：四边形ABCD是矩形；

（2）若点G为MF的中点，求证：BG是⊙O的切线；

（3）若AD=4，CM=9，求四边形ABCD的面积.

Answer 1

【答案】（1）证明见解析;（2）证明见解析; （3）S矩形ABCD=24.

【解析】试题分析：（1）根据AC为 O直径，得到∠ADC=∠CBA=90°，通过全等三角形得到CD=AB，推出四边形ABCD是平行四边形，根据矩形的判定定理得到结论；

（2）根据直角三角形的性质得到NB=MF=NF，根据等腰三角形的性质和余角的性质即可得到NB是 O的切线；

（3）根据四边形ABCD是矩形，推出△ACD∽△DMC，根据相似三角形的性质列比例式得到，从而求得DC=6,根据矩形的面积公式即可得到结论．

试题解析：

（1）证明：∵AC是⊙O的直径，

∴∠ADC=∠ABC=90°.

在Rt△ADC和Rt△CBA中，

AC=CA，AD=CB，

∴Rt△ADC≌Rt△CBA，

∴∠CAD=∠ACB，

∴AD∥BC，又AD=BC，

∴四边形ABCD是平行四边形，又∠ABC=90°，

∴□ABCD是矩形.

（2）证明：连接OB，

在Rt△MBF中，G是MF的中点，

∴BG=MF=FG，

∴∠GBF=∠GFB=∠AFE.

∵OA=OB,

∴∠OBA=∠OAB.

∵DG⊥AC，

∴∠AFE+∠OAB=90°，

∴∠GBF+∠OBA=90°，

即OB⊥BG，

∴BG是⊙O的切线.

（3）解：由（1）得四边形ABCD是矩形，

∴∠ADC=∠DCM=90°又AC⊥DG，

∴∠CDM+∠ACD=90°，∠CDM+∠M=90°

∴∠ACD=∠M

又∠ADC=∠DCM，

∴△ACD∽△DMC，

∴，

∴DC2=AD·CM=36，

∴DC=6，

∴S矩形ABCD=AD·CD=24.