题目内容
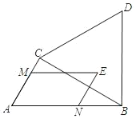
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=4,△BCD为等边三角形,点E为△BCD围成的区域(包括各边)内的一点,过点E作EM∥AB,交直线AC于点M,作EN∥AC,交直线AB于点N,则![]() AN+AM的最大值为_____.
AN+AM的最大值为_____.
【答案】5
【解析】
作辅助线,构建30度的直角三角形,即可得到结论.
过E作EH⊥AC交AC的延长线于点H,
∵EN∥AC,EM∥AB,
∴四边形ANEM是平行四边形,∠HME=∠A=60°,
设EM=AN=a,AM=b,
Rt△HEM中,∠HEM=30°,
∴MH=![]() ME=
ME=![]() a,
a,
∴![]() AN+AM=
AN+AM=![]() a+b=MH+AM=AH,
a+b=MH+AM=AH,
当E在点D时,AH的值最大是:2+3=5,
![]() AN+AM的最大值为5,
AN+AM的最大值为5,
故答案为:5.

练习册系列答案
相关题目
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为400人,如表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
图书种类 | 频数 | 频率 |
科普常识 | 1600本 | B |
名人传记 | 1280本 | 0.32 |
漫画丛书 | A本 | 0.24 |
其它 | 160本 | 0.04 |
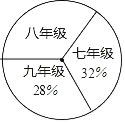
(1)求该校八年级的人数占全校总人数的百分率为 ;
(2)表中A= ,B= ;
(3)该校学生平均每人读多少本课外书?