题目内容
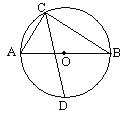
【题目】如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连结OE,CD=![]() ,∠ACB=30°.
,∠ACB=30°.
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长.

【答案】(1)证明见解析;(2)AB=2,OE=![]() .
.
【解析】
(1)根据AB是直径即可求得∠ADB=90°,再根据题意可求出OD⊥DE,即得出结论;
(2)根据三角函数的定义,即可求得BC,进而得到AB,再在Rt△CDE中,根据直角三角形的性质,可求得DE,再由勾股定理求出OE即可.
(1)连接BD,OD.
∵AB是直径,
∴∠ADB=90°.
又∵AB=BC,
∴AD=CD.
∵OA=OB,
∴OD∥BC.
∵DE⊥BC,
∴∠DEC=90°.
∵OD∥BC,
∴∠ODE=∠DEC=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
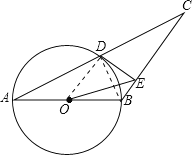
(2)在Rt△CBD中CD![]() ,∠ACB=30°,
,∠ACB=30°,
∴BC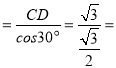 2,
2,
∴AB=2,
∴OD![]() AB=1.
AB=1.
在Rt△CDE中,CD![]() ,∠ACB=30°,
,∠ACB=30°,
∴DE![]() CD
CD![]() .
.
在Rt△ODE中,OE![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在一个不透明的袋子中装有除颜色外其余均相同的m个小球,其中8个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球实验,之后把它放回袋中,搅匀后,再继续摸出一球,记下其颜色,以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
摸出黑球次数 | 49 | 425 | 1722 | 3208 | 16698 | 33329 |
根据列表,可以估计出m的值是( )
A.8B.16C.24D.32