题目内容
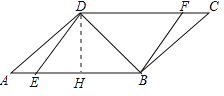
【题目】(2015南通)如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.

【答案】答案见解析.
【解析】试题分析:(1)由平行四边形的性质得到对边平行且相等,对角相等,再由垂直的定义得到一对直角相等,利用等式的性质等到一对角相等,利用ASA即可得证;
(2)过点D作DH⊥AB,在Rt△ADH中,有AD=2DH,在Rt△DEB中,有EB=2DH,易得四边形EBFD为平行四边形,利用平行四边形的对边相等得到EB=DF,等量代换即可得证.
试题解析:(1)∵四边形ABCD是平行四边形,∴AD=CB,∠A=∠C,AD//CB,
∴∠ADB=∠CBD,
∵ED⊥DB,FB⊥BD,∴∠EDB=∠FBD=90°,∴∠ADE=∠CBF,
在△AED和△CFB中,∠ADE=∠CBD,AD=BC,∠A=∠C,∴△AED≌△CFB(ASA);
(2)作DH⊥AB,垂足为H,
在R t△ADH在,∠A=30°,∴AD=2DH,
在Rt△DEB中,∠DEB=45°,∴EB=2DH,
∵∠EDB=∠FBD=90°,∴DE//BF,又∵DC//AB,∴四边形DEBF是平行四边形,
∴FD=BE,∴DA=DF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目