��Ŀ����
��2012•�㰲����ͼ����ƽ��ֱ������ϵxOy�У�AB��x���ڵ�B��AB=3��tan��AOB=
������OAB����ԭ��O��ʱ����ת90�㣬�õ���OA1B1���ٽ���OA1B1�����߶�OB1���е���ת180�㣬�õ���OA2B1��������y=ax2+bx+c��a��0��������B��B1��A2��
��1���������ߵĽ���ʽ��
��2���ڵ��������ڣ��������ϵĵ�P��ʲôλ��ʱ����PBB1�������������ʱ��P�����꣮
��3���ڵ��������ڣ����������Ƿ���ڵ�Q��ʹ��Q���߶�BB1�ľ���Ϊ
�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�

| 3 |
| 4 |
��1���������ߵĽ���ʽ��
��2���ڵ��������ڣ��������ϵĵ�P��ʲôλ��ʱ����PBB1�������������ʱ��P�����꣮
��3���ڵ��������ڣ����������Ƿ���ڵ�Q��ʹ��Q���߶�BB1�ľ���Ϊ
| ||
| 2 |

��������1�����ȸ�����ת������ȷ����B��B1��A2��������꣬Ȼ�����ô���ϵ������������ߵĽ���ʽ��
��2�������PBB1���������ʽ������һ������P�������Ķ��κ��������ö��κ�����ֵ�ķ��������PBB1��������ֵ��ֵ��ע��������PBB1����ķ�������ͼ1��ʾ��
��3�����������ˣ�2�������������������ʽ�Ľ��ۣ����ô˱���ʽ��ʾ����QBB1�������Ȼ���һԪ���η������Q������꣮
��2�������PBB1���������ʽ������һ������P�������Ķ��κ��������ö��κ�����ֵ�ķ��������PBB1��������ֵ��ֵ��ע��������PBB1����ķ�������ͼ1��ʾ��
��3�����������ˣ�2�������������������ʽ�Ľ��ۣ����ô˱���ʽ��ʾ����QBB1�������Ȼ���һԪ���η������Q������꣮
����⣺��1����AB��x�ᣬAB=3��tan��AOB=
����OB=4��
��B��-4��0����B1��0��-4����A2��3��0����
��������y=ax2+bx+c��a��0��������B��B1��A2��
��
��
���
�������ߵĽ���ʽΪ��y=
x2+
x-4��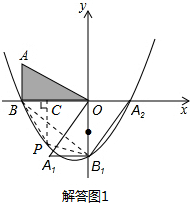
��2����P�ǵ���������������y=
x2+
x-4�ϵ�һ�㣬
���ͼ1������P��PC��x���ڵ�C��
���P��������m��n������m��0��n��0��n=
m2+
m-4��
����PC=|n|=-n=-
m2-
m+4��OC=|m|=-m��BC=OB-OC=|-4|-|m|=4+m��
S��PBB1=S��PBC+S����PB1OC-S��OBB1
=
��BC��PC+
����PC+OB1����OC-
��OB��OB1
=
����4+m������-
m2-
m+4��+
��[��-
m2-
m+4��+4]����-m��-
��4��4
=-
m2-
m=-
��m+2��2+
��m=-2ʱ����PBB1����������ʱ��n=-
������P��-2��-
����
��3��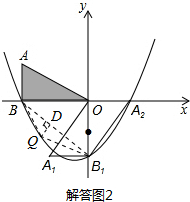 �����ڵ��������������ϴ��ڵ�Q��x0��y0����ʹ��Q���߶�BB1�ľ���Ϊ
�����ڵ��������������ϴ��ڵ�Q��x0��y0����ʹ��Q���߶�BB1�ľ���Ϊ
��
���ͼ2������Q��QD��BB1�ڵ�D��
�ɣ�2����֪����ʱ��QBB1��������Ա�ʾΪ��-
��x0+2��2+
��
��Rt��OBB1��BB1=
=4
��S��QBB1=
��BB1��QD=
��4
��
=2��
��-
��x0+2��2+
=2��
���x0=-1��x0=-3
��x0=-1ʱ��y0=-4����x0=-3ʱ��y0=-2��
��ˣ��ڵ��������ڣ��������ϴ��ڵ�Q��ʹ��Q���߶�BB1�ľ���Ϊ
�������ĵ�Q�������ǣ�-1��-4����-3��-2����
| 3 |
| 4 |
��B��-4��0����B1��0��-4����A2��3��0����
��������y=ax2+bx+c��a��0��������B��B1��A2��
��
|
���
|
�������ߵĽ���ʽΪ��y=
| 1 |
| 3 |
| 1 |
| 3 |

��2����P�ǵ���������������y=
| 1 |
| 3 |
| 1 |
| 3 |
���ͼ1������P��PC��x���ڵ�C��
���P��������m��n������m��0��n��0��n=
| 1 |
| 3 |
| 1 |
| 3 |
����PC=|n|=-n=-
| 1 |
| 3 |
| 1 |
| 3 |
S��PBB1=S��PBC+S����PB1OC-S��OBB1
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
=-
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
��m=-2ʱ����PBB1����������ʱ��n=-
| 10 |
| 3 |
| 10 |
| 3 |
��3��
 �����ڵ��������������ϴ��ڵ�Q��x0��y0����ʹ��Q���߶�BB1�ľ���Ϊ
�����ڵ��������������ϴ��ڵ�Q��x0��y0����ʹ��Q���߶�BB1�ľ���Ϊ
| ||
| 2 |
���ͼ2������Q��QD��BB1�ڵ�D��
�ɣ�2����֪����ʱ��QBB1��������Ա�ʾΪ��-
| 2 |
| 3 |
| 8 |
| 3 |
��Rt��OBB1��BB1=
| OB2+OB12 |
| 2 |
��S��QBB1=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
��-
| 2 |
| 3 |
| 8 |
| 3 |
���x0=-1��x0=-3
��x0=-1ʱ��y0=-4����x0=-3ʱ��y0=-2��
��ˣ��ڵ��������ڣ��������ϴ��ڵ�Q��ʹ��Q���߶�BB1�ľ���Ϊ
| ||
| 2 |
�����������ۺϿ����˴���ϵ�����������߽���ʽ�����κ���ͼ���ϵ������������һԪ���η��̡���ת������仯��ͼ����������ɶ�������Ҫ֪ʶ�㣮�ڣ�2������������µ����ã��DZ�����ѵ�����ģ����е�Ҫ��������ƽ����ͼ���������ⷽ�������ַ�����ѹ�����г�����һ�ֽ��ⷽ����ͬѧ����Ҫ�������գ�

��ϰ��ϵ�д�
 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
�����Ŀ
 ��2012•�㰲����ͼ��һ��������ı���չ��ͼ����ԭ���������롰���������ڵ�����Ե����ϱ�����ǣ�������
��2012•�㰲����ͼ��һ��������ı���չ��ͼ����ԭ���������롰���������ڵ�����Ե����ϱ�����ǣ������� ��2012•�㰲����ͼ����������y=
��2012•�㰲����ͼ����������y= ��2012•�㰲����ͼ��2012��4��10�գ��й��������й��Ϻ����ҵ�����������ҵ���й����ബ��A����鷢�֣�����ƫ��60�㷽���B�أ���һ��ij����������ÿСʱ13������ٶ������������C����ʻ����ͼץ������C�ز�����й�����ʱ��C��λ���й����ബ����ƫ��45�㷽���10���ﴦ���й����ബ��ÿСʱ30������ٶȸ���C�ؾ�Ԯ�ҹ������ܲ��ܼ�ʱ�ϵ�����
��2012•�㰲����ͼ��2012��4��10�գ��й��������й��Ϻ����ҵ�����������ҵ���й����ബ��A����鷢�֣�����ƫ��60�㷽���B�أ���һ��ij����������ÿСʱ13������ٶ������������C����ʻ����ͼץ������C�ز�����й�����ʱ��C��λ���й����ബ����ƫ��45�㷽���10���ﴦ���й����ബ��ÿСʱ30������ٶȸ���C�ؾ�Ԯ�ҹ������ܲ��ܼ�ʱ�ϵ����� ��2012•�㰲����ͼ����֪˫����y=
��2012•�㰲����ͼ����֪˫����y=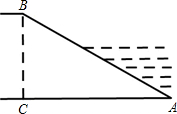 ��2012•�㰲����ͼ��ijˮ��̰Ӻ����ӭˮ��AB���±���1
��2012•�㰲����ͼ��ijˮ��̰Ӻ����ӭˮ��AB���±���1