题目内容
 (2012•广安)如图,把抛物线y=
(2012•广安)如图,把抛物线y=| 1 |
| 2 |
| 1 |
| 2 |
| 27 |
| 2 |
| 27 |
| 2 |
分析:根据点O与点A的坐标求出平移后的抛物线的对称轴,然后求出点P的坐标,过点P作PM⊥y轴于点M,根据抛物线的对称性可知阴影部分的面积等于矩形NPMO的面积,然后求解即可.
解答: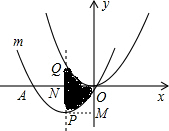 解:过点P作PM⊥y轴于点M,
解:过点P作PM⊥y轴于点M,
∵抛物线平移后经过原点O和点A(-6,0),
∴平移后的抛物线对称轴为x=-3,
得出二次函数解析式为:y=
(x+3)2+h,
将(-6,0)代入得出:
0=
(-6+3)2+h,
解得:h=-
,
∴点P的坐标是(-3,-
),
根据抛物线的对称性可知,阴影部分的面积等于矩形NPMO的面积,
∴S=|-3|×|-
|=
.
故答案为:
.
 解:过点P作PM⊥y轴于点M,
解:过点P作PM⊥y轴于点M,∵抛物线平移后经过原点O和点A(-6,0),
∴平移后的抛物线对称轴为x=-3,
得出二次函数解析式为:y=
| 1 |
| 2 |
将(-6,0)代入得出:
0=
| 1 |
| 2 |
解得:h=-
| 9 |
| 2 |
∴点P的坐标是(-3,-
| 9 |
| 2 |
根据抛物线的对称性可知,阴影部分的面积等于矩形NPMO的面积,
∴S=|-3|×|-
| 9 |
| 2 |
| 27 |
| 2 |
故答案为:
| 27 |
| 2 |
点评:本题考查了二次函数的问题,根据二次函数的性质求出平移后的抛物线的对称轴的解析式,并对阴影部分的面积进行转换是解题的关键.

练习册系列答案
相关题目
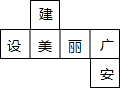 (2012•广安)如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
(2012•广安)如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( ) (2012•广安)如图,2012年4月10日,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(
(2012•广安)如图,2012年4月10日,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?( (2012•广安)如图,已知双曲线y=
(2012•广安)如图,已知双曲线y=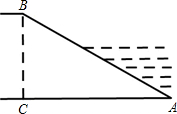 (2012•广安)如图,某水库堤坝横断面迎水坡AB的坡比是1
(2012•广安)如图,某水库堤坝横断面迎水坡AB的坡比是1