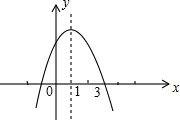题目内容
已知抛物线y=ax2+bx+c(a>0)的顶点是C(0,1),直线l:y=-ax+3与这条抛物线交于P、Q两点,与x轴、y轴分别交于点M和N。
(1)设点P到x轴的距离为2,试求直线l的函数关系式;
(2)若线段MP与PN的长度之比为3:1,试求抛物线的函数关系式。
(1)设点P到x轴的距离为2,试求直线l的函数关系式;
(2)若线段MP与PN的长度之比为3:1,试求抛物线的函数关系式。
解:(1)∵抛物线的顶点是C(0,1),∴b=0,c=1,
如图1,
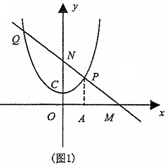
∵a>0,直线l过点N(0,3)
∴M点在x轴正半轴上
∵点P到x轴的距离为2,即点P的纵坐标为2。
把y=2代入 得,
得,
∴P点坐标为( ,2)
,2)
∵直线与抛物线交于点P
∴点P在 上,
上,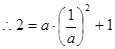
∴a=1
∴直线l的函数关系式为
(2)如图2,若点P在y轴的右边,记为P1,过点P1作P1A⊥x轴于A,

 ,
,
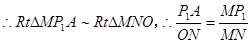
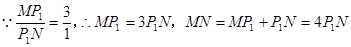 ,
,
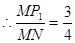 ,即
,即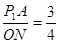
∵ON=3, ,即点P1的纵坐标为
,即点P1的纵坐标为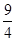
把 代入
代入 ,得
,得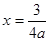
∴点P1的坐标为( )
)
又∵点P1是直线l与抛物线的交点。∴点P1在抛物线 上,
上,
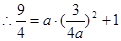

∴抛物线的函数关系式为
如图2,若点P在y轴的左边,记为P2。作P2B⊥x轴于B

 。
。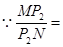
 ,
,
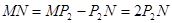 ,
,
 ,即
,即
∵ON=3,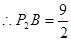 ,即点P2的纵坐标为
,即点P2的纵坐标为
由P2在直线l上可求得
又∵P2在抛物线上,
∴抛物线的函数关系式为

如图1,

∵a>0,直线l过点N(0,3)
∴M点在x轴正半轴上
∵点P到x轴的距离为2,即点P的纵坐标为2。
把y=2代入
 得,
得,
∴P点坐标为(
 ,2)
,2) ∵直线与抛物线交于点P
∴点P在
 上,
上,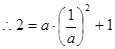
∴a=1
∴直线l的函数关系式为

(2)如图2,若点P在y轴的右边,记为P1,过点P1作P1A⊥x轴于A,

 ,
,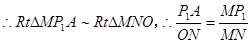
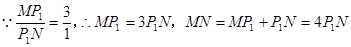 ,
,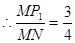 ,即
,即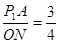
∵ON=3,
 ,即点P1的纵坐标为
,即点P1的纵坐标为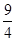
把
 代入
代入 ,得
,得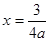
∴点P1的坐标为(
 )
) 又∵点P1是直线l与抛物线的交点。∴点P1在抛物线
 上,
上,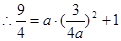

∴抛物线的函数关系式为

如图2,若点P在y轴的左边,记为P2。作P2B⊥x轴于B

 。
。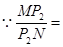
 ,
,
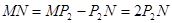 ,
, ,即
,即
∵ON=3,
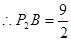 ,即点P2的纵坐标为
,即点P2的纵坐标为
由P2在直线l上可求得

又∵P2在抛物线上,

∴抛物线的函数关系式为

(1)由于抛物线的顶点为C(0,1),因此抛物线的解析式中b=0,c=1.即抛物线的解析式为y=ax2+1.已知了P到x轴的距离为2,即P点的纵坐标为2.可根据直线l的解析式求出P点的坐标,然后将P点坐标代入抛物线的解析式中即可求得a的值,也就能求出直线l的函数关系式.
(2)本题要根据相似三角形来求.已知了线段MP与PN的长度之比为3:1,如果过P作x轴的垂线,根据平行线分线段成比例定理即可得出P点的纵坐标的值.进而可仿照(1)的方法,先代入直线的解析式,然后再代入抛物线中即可求出a的值,也就求出了抛物线的解析式
(2)本题要根据相似三角形来求.已知了线段MP与PN的长度之比为3:1,如果过P作x轴的垂线,根据平行线分线段成比例定理即可得出P点的纵坐标的值.进而可仿照(1)的方法,先代入直线的解析式,然后再代入抛物线中即可求出a的值,也就求出了抛物线的解析式

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).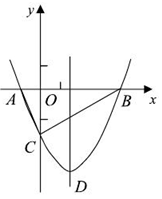
 ,直线
,直线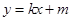 的图象与该二次函数的图象交于
的图象与该二次函数的图象交于 两点,其中
两点,其中 点坐标为
点坐标为 ,
,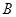 点在
点在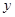 轴上,直线与
轴上,直线与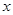 轴的交点为
轴的交点为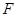 .
.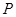 为线段
为线段 上的一个动点(点
上的一个动点(点 点.
点. 的值及这个二次函数的解析式;
的值及这个二次函数的解析式;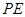 的长为
的长为 ,点
,点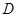 为直线
为直线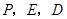 为顶点的三角形与
为顶点的三角形与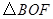 相似?若存在,请求出
相似?若存在,请求出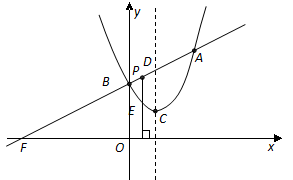
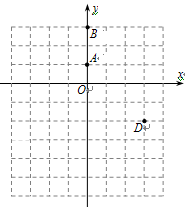
 ,A与
,A与 上,且这条抛物线与
上,且这条抛物线与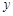 轴的交点的纵坐标为-6,求这条抛物线的顶点坐标.
轴的交点的纵坐标为-6,求这条抛物线的顶点坐标. ,1),有下列结论:①ac<0;②a+b=0;③4ac-b2>4a;④a+b+c<0.其中正确的结论有( )
,1),有下列结论:①ac<0;②a+b=0;③4ac-b2>4a;④a+b+c<0.其中正确的结论有( )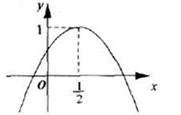
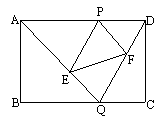
 中,
中,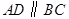 ,
, ,
, ,点
,点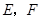 分别在线段
分别在线段 上(点
上(点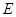 与点
与点 不重合),且
不重合),且 ,设
,设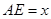 ,
, .
.
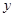 与
与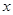 的函数表达式;
的函数表达式;