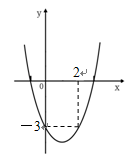题目内容
如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点. 连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.

(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?
(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)

(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?
(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)
(1)证∠APE=∠ADQ,∠AEP=∠AQD.
(2)注意到△APE∽△ADQ与△PDE∽△ADQ,及S△PEF= ,
,
得S△PEF= =
= . ∴当
. ∴当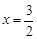 ,即P是AD的中点时,S△PEF取得最大值
,即P是AD的中点时,S△PEF取得最大值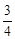 .
.
(3)作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点.
(2)注意到△APE∽△ADQ与△PDE∽△ADQ,及S△PEF=
 ,
,得S△PEF=
 =
= . ∴当
. ∴当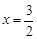 ,即P是AD的中点时,S△PEF取得最大值
,即P是AD的中点时,S△PEF取得最大值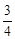 .
.(3)作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点.
(1)证得∠APE=∠ADQ,∠AEP=∠AQD,即可得到△APE∽△ADQ;
(2)先由△APE∽△ADQ与△PDE∽△ADQ,及S△PEF= ,
,
得S△PEF= =
= ,根据二次函数的性质即可结果;
,根据二次函数的性质即可结果;
(3)作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点.
(2)先由△APE∽△ADQ与△PDE∽△ADQ,及S△PEF=
 ,
,得S△PEF=
 =
= ,根据二次函数的性质即可结果;
,根据二次函数的性质即可结果;(3)作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,此时Q是BC的中点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 每亩树苗的收益)
每亩树苗的收益) ,
, )
) 经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m,
经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m, ),点C是抛物线在第三象限的一点,且横坐标为-2.
),点C是抛物线在第三象限的一点,且横坐标为-2.
 ,
,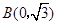 ,
,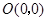 ,将此三角板绕原点
,将此三角板绕原点 顺时针旋转
顺时针旋转 ,得到
,得到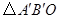 .
. ,求该抛物线解析式;
,求该抛物线解析式; 是在第一象限内抛物线上一动点,求使四边形
是在第一象限内抛物线上一动点,求使四边形 的面积达到最大时点
的面积达到最大时点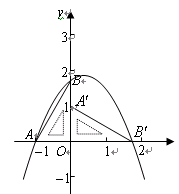
 的图象经过
的图象经过 和
和 两点,且交
两点,且交 轴于点
轴于点 .
. 、
、 的值;
的值; 轴交抛物线于点
轴交抛物线于点 点
点 为此抛物线的顶点,试确定
为此抛物线的顶点,试确定 的形状.
的形状.

 的y与x的部分对应值如下表:
的y与x的部分对应值如下表: 的正根在3与4之间
的正根在3与4之间 图象的顶点坐标是 _ __ __.
图象的顶点坐标是 _ __ __. 的图象如图所示,则
的图象如图所示,则 的值是( )
的值是( )