题目内容
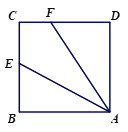
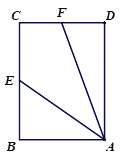
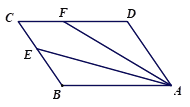
【题目】在矩形ABCD中，F为AD的中点，DE＝
，CF⊥BD分别交BD，AD于点E，F，连接BF.
（1）求证：EC＝2EF；
（2）求四边形BCDF的面积.
【答案】（1）见解析；（2）
【解析】分析：由在矩形ABCD中，AD∥BC，可得FD：BC＝FE：EC，又由F为AD的中点，即可证FE：EC＝1：2，故可得结论；
（2）由在矩形ABCD中，CF⊥BD，可得∠DEC=∠FDC=90°，又由∠DCE=∠FCD，即可证得△DEC∽△FDC；根据已知可求出
，
，从而可求出四边形BCDF的面积.
详解：（1）证明：∵四边形ABCD为矩形，
∴AD∥BC，
∵F为AD的中点
∴FD：BC＝FE：EC＝1：2
∴EC＝2EF
（2）在矩形ABCD中，∠FDC=90°，CF⊥BD，
∴∠DEC=∠FDC=90°，
∵∠DCE=∠FCD，
∴△DEC∽△FDC；
∴
∵DE=
，EC=2EF
∴，
∴CD=
，
=
练习册系列答案
相关题目
