Question

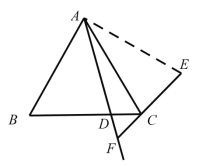
【题目】如图，在等边△ABC 中，点 D 是线段 BC 上一点.作射线 AD ，点 B 关于射线 AD 的对称点为 E .连接 EC 并延长，交射线 AD 于点 F .

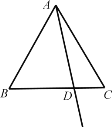
（1）补全图形；（2）求∠AFE 的度数；（3）用等式表示线段 AF 、CF 、 EF 之间的数量关系，并证明.

Answer 1

【答案】（1）答案见解析；（2）60°；（3）AF=EF+CF，理由见解析

【解析】

（1）根据题意补全图形即可；

（2）连接AE，根据对称性得到AE AB ， FAB FAE ，设FAC ，则FAB FAE 60 ，故EAC 60 60 2，再根据AE AC 得到AFE 180 FAE FEA 60；

（3）作FCG 60 交 AD 于点 G，连接 BF，根据等边三角形的性质得到ACG 60 GCD BCF，再证明△ ACG ≌△ BCF，得到AG BF，再根据对称性得到BF EF 再得到AF EF CF

（1）补全图形：

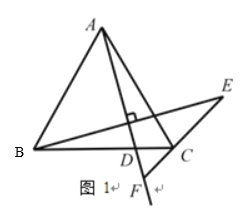
（2）连接AE，

∵△ABC 是等边三角形，

∴ AB AC BC ， BAC BCA 60.

∵点B关于射线 AD 的对称点为 E ，

∴ AE AB ，FAB FAE .

设FAC ，则FAB FAE 60

∴ EAC 60 60 2， 又 AE AC .

∴ AFE 180 FAE FEA 60

（3） AF EF CF

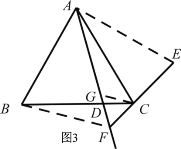
证明：如图 3，作FCG 60 交 AD 于点 G，连接 BF.

∴△ FCG 是等边三角形.

∴ GF CF GC . CGF GFC FCG 60 .

∴ACG 60 GCD BCF

在△ ACG 和△ BCF 中，

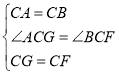
∴△ ACG ≌△ BCF .

∴ AG BF .

∵点 B 关于射线 AD 的对称点为 E ，

∴ BF EF .

∵ AF AG GF .

∴ AF EF CF