题目内容
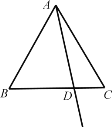
【题目】在△ABC中,AB>BC,直线l垂直平分AC.

(1)如图1,作∠ABC的平分线交直线l于点D,连接AD,CD.
①补全图形;
②判断∠BAD和∠BCD的数量关系,并证明.
(2)如图2,直线l与△ABC的外角∠ABE的平分线交于点D,连接AD,CD.求证:∠BAD=∠BCD.
【答案】(1)①见解析;②∠BAD+∠BCD=180°,证明见解析;(2)见解析.
【解析】
(1)①根据题意画图即可补全图形;
②过点D作DE⊥AB于点E、DF⊥BC交BC的延长线于点F,如图4,根据角平分线的性质和线段垂直平分线的性质可得DE=DF,DA=DC,再根据HL可证Rt△ADE≌Rt△CDF,进而可得∠BAD=∠DCF,进一步即可得出∠BAD和∠BCD的数量关系;
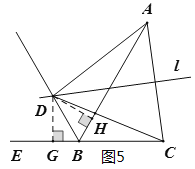
(2)过点D作DH⊥AB于点H,DG⊥CE于点G,如图5,根据角平分线的性质和线段垂直平分线的性质可得DG=DH,DA=DC,再根据HL可证Rt△ADH≌Rt△CDG,进一步即可得出结论.
解:(1)①补全图形如图3;
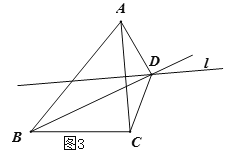
②∠BAD+∠BCD=180°.
证明:过点D作DE⊥AB于点E、DF⊥BC交BC的延长线于点F,如图4,
∵BD平分∠ABC,∴DE=DF,
∵直线l垂直平分AC,∴DA=DC,
∴Rt△ADE≌Rt△CDF(HL),∴∠BAD=∠DCF,
∵∠DCF+∠BCD=180°,
∴∠BAD+∠BCD=180°;
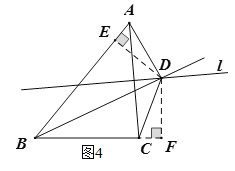
(3)证明:过点D作DH⊥AB于点H,DG⊥CE于点G,如图5,
∵BD平分∠ABE,∴DH=DG,
∵直线l垂直平分AC,∴DA=DC,
∴Rt△ADH≌Rt△CDG(HL),
∴∠BAD=∠BCD,

【题目】甲、乙、丙三位运动员在相同条件下各射靶![]() 次,每次射靶的成绩如下:
次,每次射靶的成绩如下:
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
丙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 |
|
| __________ |
乙 | __________ |
|
|
丙 |
| __________ |
|
(2)根据表中数据分析,哪位运动员的成绩最稳定.并简要说明理由.