题目内容
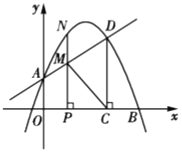
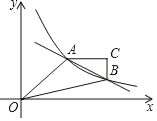
【题目】如图,在平面直角坐标系中,一次函数y=﹣![]() x+3的图象与反比例函数y=
x+3的图象与反比例函数y=![]() (x>0,k是常数)的图象交于A(a,2),B(4,b)两点.
(x>0,k是常数)的图象交于A(a,2),B(4,b)两点.
(1)求反比例函数的表达式;
(2)点C是第一象限内一点,连接AC,BC,使AC∥x轴,BC∥y轴,连接OA,OB.若点P在y轴上,且△OPA的面积与四边形OACB的面积相等,求点P的坐标.
【答案】(1) 反比例函数的表达式为y=![]() (x>0);(2) 点P的坐标为(0,4)或(0,﹣4)
(x>0);(2) 点P的坐标为(0,4)或(0,﹣4)
【解析】
(1)根据点A(a,2),B(4,b)在一次函数y=﹣![]() x+3的图象上求出a、b的值,得出A、B两点的坐标,再运用待定系数法解答即可;
x+3的图象上求出a、b的值,得出A、B两点的坐标,再运用待定系数法解答即可;
(2)延长CA交y轴于点E,延长CB交x轴于点F,构建矩形OECF,根据S四边形OACB=S矩形OECF﹣S△OAE﹣S△OBF,设点P(0,m),根据反比例函数的几何意义解答即可.
(1)∵点A(a,2),B(4,b)在一次函数y=﹣![]() x+3的图象上,
x+3的图象上,
∴﹣![]() a+3=2,b=﹣
a+3=2,b=﹣![]() ×4+3,
×4+3,
∴a=2,b=1,
∴点A的坐标为(2,2),点B的坐标为(4,1),
又∵点A(2,2)在反比例函数y=![]() 的图象上,
的图象上,
∴k=2×2=4,
∴反比例函数的表达式为y=![]() (x>0);
(x>0);
(2)延长CA交y轴于点E,延长CB交x轴于点F,
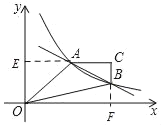
∵AC∥x轴,BC∥y轴,
则有CE⊥y轴,CF⊥x轴,点C的坐标为(4,2)
∴四边形OECF为矩形,且CE=4,CF=2,
∴S四边形OACB=S矩形OECF﹣S△OAE﹣S△OBF
=2×4﹣![]() ×2×2﹣
×2×2﹣![]() ×4×1
×4×1
=4,
设点P的坐标为(0,m),
则S△OAP=![]() ×2|m|=4,
×2|m|=4,
∴m=±4,
∴点P的坐标为(0,4)或(0,﹣4).

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.