题目内容
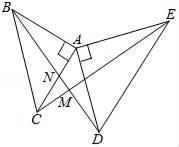
【题目】如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N.证明:
(1)△ABD≌△ACE
(2)BD⊥CE.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)求出∠BAD=∠CAE,再利用“边角边”证明即可;
(2)根据全等三角形对应角相等可得∠ADB=∠AEC,然后求出∠DEM+∠MDE=90°,再根据三角形的内角和等于180°求出∠DME=90°,最后根据垂直的定义证明即可.
试题解析:证明:(1)∵△ABC和△ADE都是等腰直角三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△ABD和△ACE中,∵AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,∴∠ADB=∠AEC,∴∠DEM+∠MDE=∠DEM+∠ADB+∠ADE=∠DEM+∠AEC+∠ADE=∠DAE+∠ADE=90°,在△DEM中,∠DME=180°﹣(∠DEM+∠MDE)=180°﹣90°=90°,∴BD⊥CE.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目