题目内容
【题目】如图,在平面直角坐标系中, ![]() 是边长为
是边长为![]() 的等边三角形,直线
的等边三角形,直线![]() 与
与![]() 轴、
轴、![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() 、
、![]() .
. ![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(![]() )点
)点![]() 的坐标为__________.(结果保留根号)
的坐标为__________.(结果保留根号)
(![]() )求证:点
)求证:点![]() 、
、![]() 关于
关于![]() 轴对称.
轴对称.
(![]() )若
)若![]() ,求直线
,求直线![]() 对应的函数表达式.
对应的函数表达式.

【答案】(![]() )
)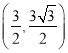 .(
.(![]() )证明见解析.(
)证明见解析.(![]() )
)![]()
【解析】试题分析:(1)过点A作AM⊥x轴于点M,根据等边三角形的性质可知:AO=3,∠AOM=60°,在Rt△AMO中利用30°角的对边为斜边的一半结合勾股定理可求出AM、OM的长,从而得出点A的坐标;
(2)由EF∥OA利用平行线的性质可得出∠BFE=∠BOA=60°,结合∠OBA=60°可得出△BEF为等边三角形,根据等边三角形的性质即可得出BE=BF可得出BE=BF、BO=BA,进而即可得出AE=OF,再由OC=AE即可得出OC=OF,从而证出点C、F关于y轴对称;
(3)设OC=OF=x,根据边与边的关系找出∠OCD=∠ODC,再根据平行线的性质即可得出∠CEF=∠CDO=∠ECF,进而可得出CF=EF,由此即可得出关于x的一元一次方程,解方程即可求出x的值,进而可得出点C、D的坐标,利用待定系数法即可求出直线l对应的函数表达式.
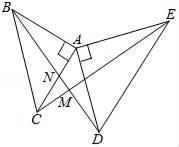
试题解析:解:(1)过点A作AM⊥x轴于点M,如图1所示.
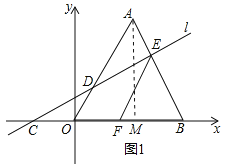
∵△A0B是边长为3的等边三角形,∴AB=OB=OA=3,且∠AOM=60°.
在Rt△AMO中,OA=3,∠AOM=60°,∴∠OAM=30°,∴OM=![]() OA=
OA=![]() ,AM=
,AM=![]() =
=![]() ,∴点A的坐标为(
,∴点A的坐标为(![]() ,
, ![]() ).
).
(2)证明:若证C、F关于y轴对称,只需证OC=OF即可.
∵EF∥OA,∴∠BFE=∠BOA=60°,∵∠OBA=60°,∴△BEF为等边三角形,∴BE=BF.
∵△AOB是等边三角形,∴BO=BA,∴AE=AB﹣BE=OB﹣BE=OF,又∵0C=AE,∴OC=OF,∴点C、F关于y轴对称.
(3)设OC=OF=x,∵OB=3,∴BF=EF=3﹣x,∵AD=EF,∴AD=3﹣x.
∵OA=3,∴OD=x,∴∠OCD=∠ODC.
∵OA∥EF,∴∠CEF=∠CDO=∠ECF,∴EF=CF,即3﹣x=2x,解得:x=1,∴点C的坐标为(﹣1,0),点D的坐标为(![]() ,
, ![]() ).
).
设直线l对应的函数表达式为y=kx+b,将点C(﹣1,0)、点D(![]() ,
, ![]() )代入直线l对应的函数表达式中,得
)代入直线l对应的函数表达式中,得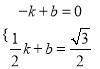 ,解得:
,解得: 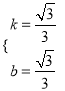 .
.
故直线l对应的函数表达式为![]() .
.

 同步奥数系列答案
同步奥数系列答案