题目内容

已知an=
1
(n+1)2
（n=1，2，3，…），我们又定义b1=2（1-a1）=
3
2
，b2=2（1-a1）（1-a2）=
4
3
，b3=2（1-a1）（1-a2）（1-a3）=
5
4
，…，根据你观察的规律可推测出bn=（　　）
A、
n+1
n
B、
n+2
n+1
C、
n+3
n+2
D、
n+1
n+2
考点：规律型：数字的变化类
专题：
分析：由b1=2（1-a1）=
3
2
，b2=2（1-a1）（1-a2）=
4
3
，b3=2（1-a1）（1-a2）（1-a3）=
5
4
…可以看出第n个数的分子是n+2，分母是n+1，由此得出答案即可．
解答：解：b1=2（1-a1）=
3
2
，
b2=2（1-a1）（1-a2）=
4
3
，
b3=2（1-a1）（1-a2）（1-a3）=
5
4
，
…
bn=
n+2
n+1
．
故选：B．
点评：此题考查数字的变化规律，找出数字之间的联系，找出规律，解决问题．
练习册系列答案
相关题目
用操作计算器的方法计算（205）2，第5个按键是（　　）
A、B、C、D、
计算-a2+3a2的结果为（　　）
A、2a2B、-2a2C、4a2D、-4a2
如图，将1、
2
、、
3
三个数按图中方式排列，若规定（a，b）表示第a排第b列的数，则（8，2）与（2014，2014）表示的两个数的积是（　　）
A、
6
B、
3
C、
2
D、1
现规定正整数n的“N运算”是：
①当n为奇数时，N=3n+1；
②当n为偶数时，N=n×
1
2
×
1
2
…（其中N为奇数）．
如：数3经过1次“N运算”的结果是10，经过2次“N运算”的结果为5，经过3次“N运算”的结果为16，经过4次“N运算”的结果为1，则数7经过2014次的“N运算”得到的结果是（　　）
A、1B、4C、5D、16
给定一列按规律排列的数：1，
4
3
，
3
2
，
8
5
，…，则这列数的第9个数是（　　）
A、
9
10
B、
9
5
C、
16
9
D、
20
11
如图是一串有趣的图案按一定的规律排列，请仔细观察，按此规律第2014个图案是（　　）
A、B、C、D、
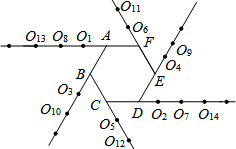将正六边形ABCDEF的各边按如图所示延长，从射线FA开始，分别在各射线上标记点O1，O2，O3，…，按此规律，则点O2013所在射线是（　　）
A、ABB、DEC、BCD、EF
将图中的图形绕着直线l旋转一周得到的几何体是（　　）
A、B、C、D、

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网